三维人体动捕模型 SMPL:A Skinned Multi Person Linear Model
在人体动作捕捉(motion capture)领域,SMPL 算法最为常见,它是由德国马普所提出的一种参数化的三维人体动捕模型,具有通用性、易于渲染和兼容现有商业软件(比如 UE4 和 Unity)的优点。
「这是一篇鸽了很久的文章,今天补上。」
1. 人体动捕介绍
1.1 动作捕捉技术
目前人体动作捕捉技术在影视制作和游戏领域已经应用得很成熟了,最常见的就是基于可穿戴设备(比如 IMU)的人体动捕技术。当动作人做出运动时,穿戴的传感器会捕捉人体的姿态数据并回传给虚拟角色,进而驱动虚拟角色做出与动作人相同的角色。
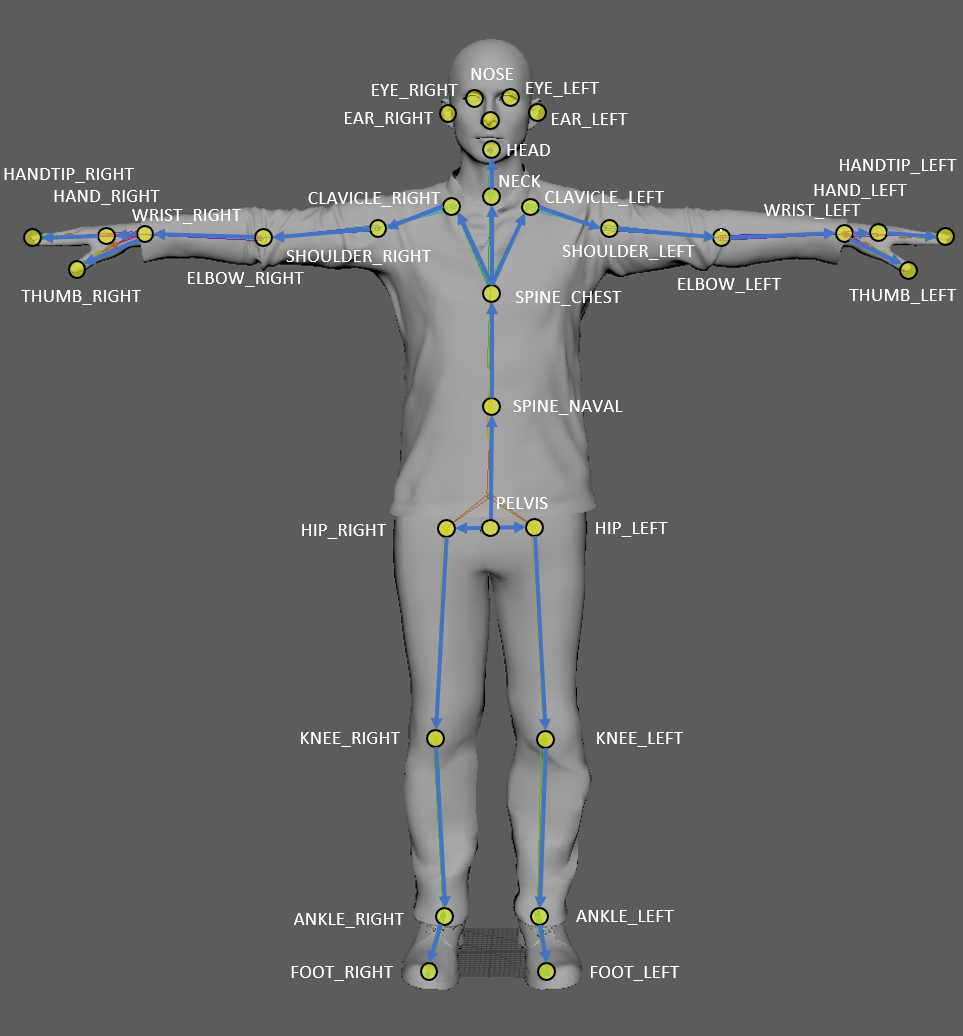
| Index | Joint name | Parent joint |
|---|---|---|
| 0 | PELVIS | - |
| 1 | SPINE_NAVAL | PELVIS |
| 2 | SPINE_CHEST | SPINE_NAVAL |
| … | … | … |
如下图所示:每个关节点都有一套自己的坐标系,当人体在运动时,每个关节点就会相对其父节点发生旋转,这个旋转过程可以用一个四元数表达。如果两套虚拟形象的关节点坐标系朝向不一致,那么还需要进行一些适配工作(相当枯燥乏味)。

1.2 线性混合蒙皮
SMPL 涉及到游戏制作和渲染技术里面的一些东西,特别是计算机图形学领域。考虑到 SMPL 是在 LBS(Linear Blending Skinning,线性混合蒙皮)的基础上开发的,因此先对 LBS 做个简单的介绍。
对于一个虚拟形象,其实可以大致分为两大块:骨架(bones)和表皮(skin)。骨架一般由一套关节树(skeleton tree)构成,表皮则由一系列的网格顶点(vertices)组成,每个 vertices 都有坐标位置 xyz,然后这些 vertices 就组成了面(也就是表皮)。 在虚拟形象的美术制作过程中,通常是先制作出一套骨架,然后将这些网格顶点(皮)在 rest-pose 状态下按照一定的权重绑定在每个关节上,这个过程我们称之为蒙皮(skinning)。
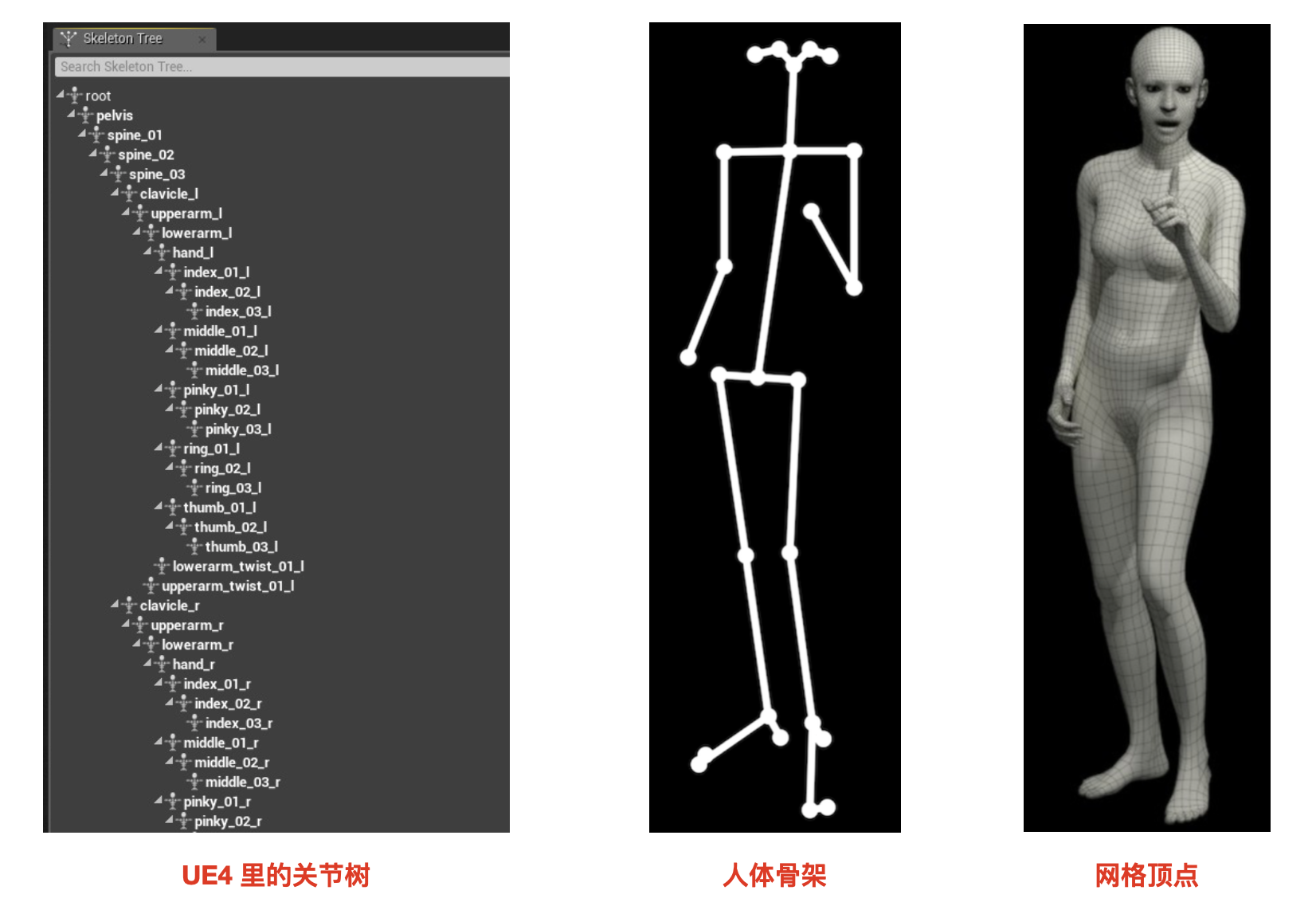
当虚拟形象发生运动时,骨骼的每个关节也会发生相应的旋转和位移,这个时候所绑定的网格顶点就需要根据每个绑定的关节点的影响加权求和算出运动后的位置。由于整个过程都是可以通过矩阵的线性运算得到,并且考虑到了所有关节点的混合影响,因此称为线性混合蒙皮。
LBS 主要是用来计算蒙皮后的网格顶点位置,假设虚拟人物一共有 {1,2,3,...,m} 个关节点,n 个网格顶点,其数学表达式如下:
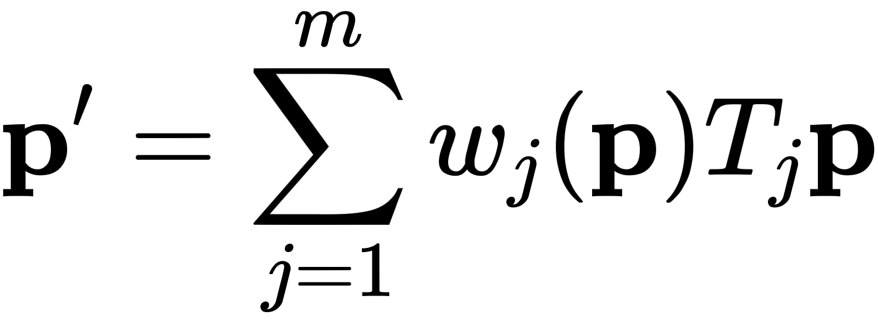
p' 为蒙皮后的网格顶点新位置,维度为 [n, 3];w 为权重矩阵,维度为 [n, m];T 则是每个关节点的仿射变换矩阵,维度为 [m, 4, 4],该矩阵代表了关节点的旋转和平移;p 为蒙皮前的网格顶点位置。
2. SMPL 模型
2.1 SMPL 的背景
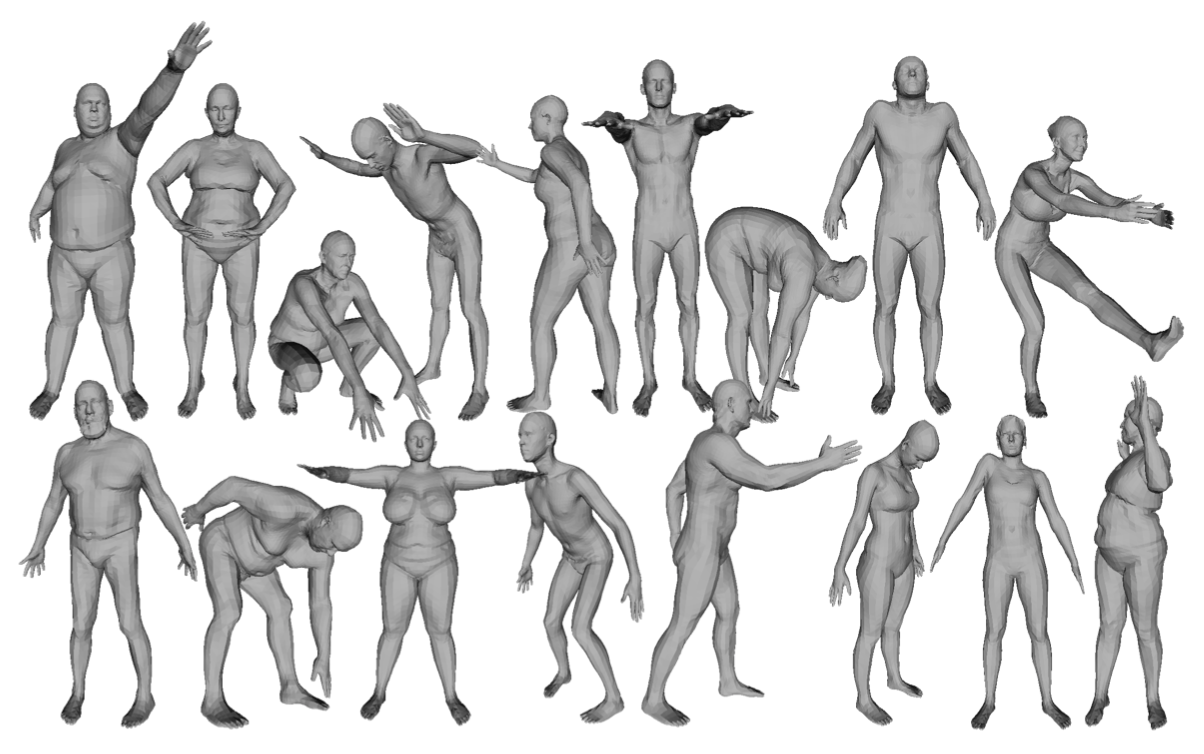
LBS 面临的一个难点是:线性混合蒙皮算法会出现皮肤塌陷和皱褶的问题,作者称之为 “taffy”(太妃糖) 和 “bowtie”(领结)。比如下图中当手臂弯曲的时候,LBS 的效果(青绿色)就折叠得比较夸张,而且在关节连接处不能提供平滑自然的过渡。目前商业上普遍的做法是通过人工绑定(rigging)和手工雕刻 blend shape 来改善这个问题,这个过程会比较耗费人力。

SMPL 较好地解决了上述的痛点,并且一开始的出发点就是为了提出业界兼容、简单易用和渲染速度快的三维人体重建模型,作者认为像这种以往需要人工绑定(rigging)和手工雕刻 blend shape 的过程其实是可以通过大量数据学习得到。
2.2 SMPL 参数定义
SMPL 模型一共定义了 N=6890 个 vertices 和 K=23 个 joints,并且通过以下两类统计参数对人体进行描述。
体型参数 β:拥有 10 个维度去描述一个人的身材形状,每一个维度的值都可以解释为人体形状的某个指标,比如高矮,胖瘦等。
姿态参数 θ:拥有 24×3 个维度去描述人体的动作姿态,其中 24 指的是 23 个关节点 + 1 个根结点,3 则指的是轴角(axis-angle)里的数值。
在 python 代码中,我们可以这样随机设置 SMPL 参数:
# 设置身材参数 betas 和姿态参数 poses |
2.3 SMPL 的过程
SMPL 过程主要可以分为以下三大阶段:
1. 基于形状的 blend shape (混合变形)
人体的网格顶点(vertices)会随着 shape 参数 β 变化而变化,这个变化过程是在一个基模版(或者称之为统计上的均值模版,mean template)上线性叠加的。关于这个线性叠加偏量,作者使用了 Bs(β) 函数来计算:
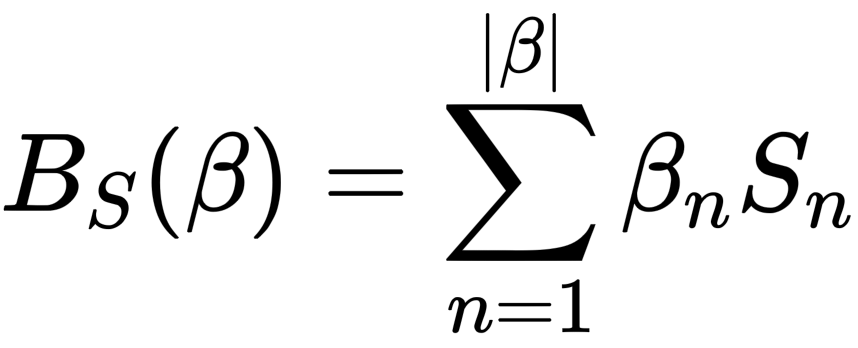
它表示每个 shape 参数对 vertices 的影响。其中 S (对应 smpl['shapedirs'])是通过数据学习出来的,它的维度为 (6890, 3, 10)。
# 根据 betas 调整 T-pose, 计算 vertices |
2. 基于姿态的 blend shape
前面计算的是人体在静默姿态(T-pose)下的 blend shape,这里将计算人体在不同 pose 参数 θ 下的影响。同样的定义了一个函数 Bp(θ) 计算该线性叠加偏量:
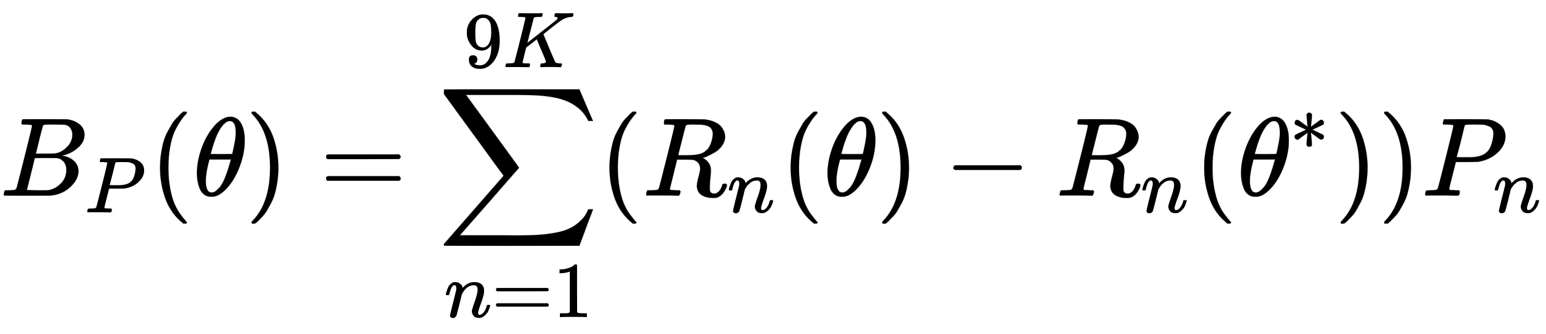
在上面公式中,因为我们是计算相对 T-pose 状态下的线性叠加偏量,所以人体的位姿应该也是要相对 T-pose 状态下进行变化,因此括号里减去了 T-pose 位姿的影响。每个 pose 参数都用旋转矩阵 R 表示,所以是 9K。同样 P (即权重矩阵,对应 smpl['posedirs'])也是通过数据学习出来的,它的维度为 (6890, 3, 207),其中 207 是因为 23x9 得到。
def posemap(p): |
3. 蒙皮过程(blend skinning)
当人体关节(joint)运动时,由网格顶点(vertex)组成的“皮肤”将会随着关节的运动而变化,这个过程称之为蒙皮。蒙皮过程可以认为是皮肤节点随着关节的变化而产生的加权线性组合。简单来说,就是距离某个具体的关节越近的端点,其跟随着该关节旋转/平移等变化的影响越强。
由于输入的 pose 参数是每个子关节点相对父关节点进行旋转的( relative rota- tion of part k with respect to its parent in the kinematic tree),因此需要计算每个关节坐标系变换到相机坐标系的 transform 矩阵 T:
rodrigues = lambda x: cv2.Rodrigues(x)[0] |
在人体动作捕捉领域中,描述人体关节点的刚性运动指的是每个关节点在运动时相对于静默姿态(T-pose)时的旋转平移。例如对于左腿抬起这样一个动作,1 号节点 L_HIP 可以通过 T1 矩阵从静默姿态变换到该姿态,并且底下的子节点都会发生相应的变换(这在上一步骤子节点乘上父节点的变换矩阵已体现)。
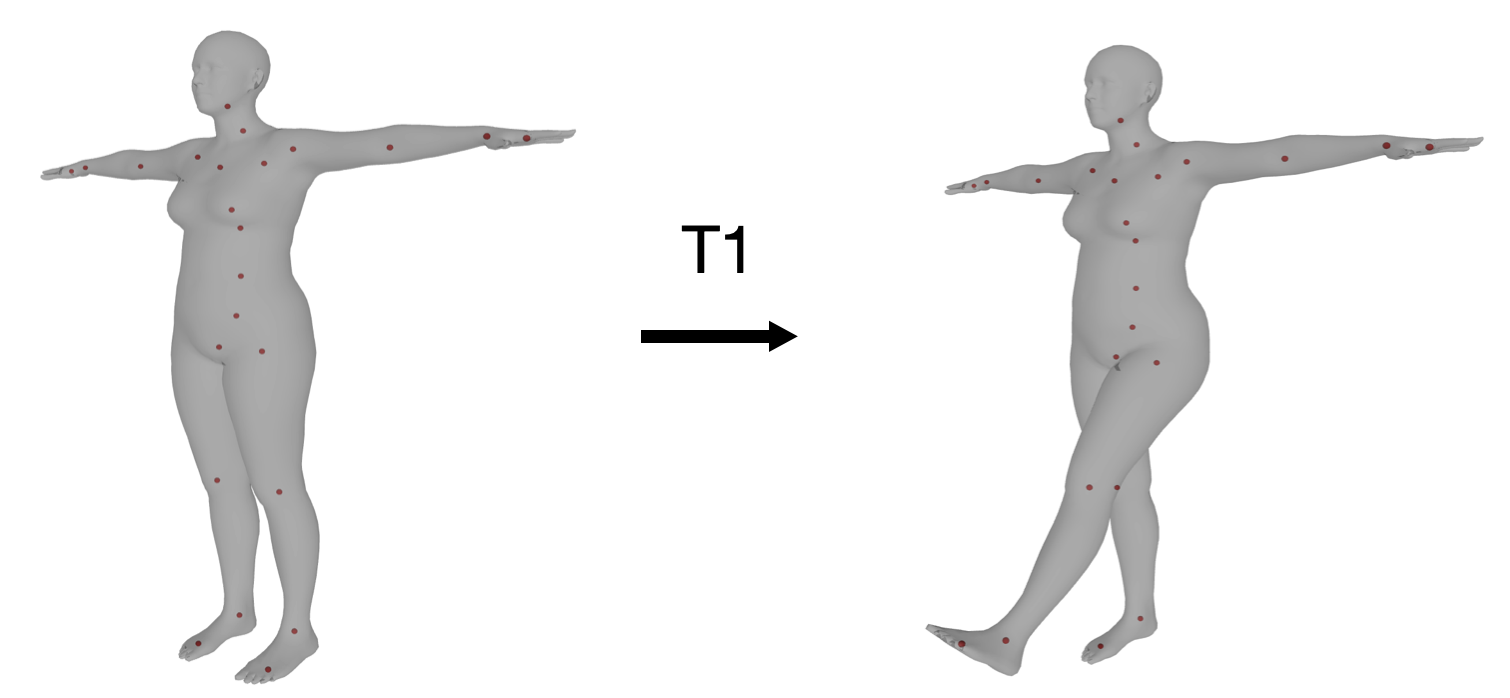
由于 SMPL 模型的子节点在 T-pose 状态下坐标系的朝向和相机坐标系相同,因此旋转矩阵不用发生变化, 只需要减去 T-pose 时的关节点位置得到相对偏移量就行:
# 计算每个子节点相对 T-pose 时的位姿矩阵 |
以上 Ts 就是各个子节点相对各自在 T-pose 情况下的变换矩阵(transform matrix),该矩阵可以使得每个 vertices 在 T-pose 状态下的位置映射到发生运动时的新位置。蒙皮时还要考虑所有关节对每个 vertice 的加权影响,因此乘上一个维度为 (6890, 24) 的加权矩阵 smpl['weights']:
# 开始蒙皮操作,LBS 过程 |
在得到网格顶点 vertices 后,还可以通过乘上一个 J_regressor 矩阵(通过大量数据学习得到)得到每个关节点的位置 joints (与 global_joints 的值基本相同):
joints = smpl['J_regressor'].dot(vertices) # 计算 pose 下 joints 位置,其值基本与 global_joints 一致 |
2.4 3D 到 2D 投影
上述过程中计算得到的网格顶点 vertices 和 joints 位置,都是在相机坐标系内。在一些相关的 SMPL 算法(如 vibe 和 expose)中,SMPL 的相机内参都是假定为:
fx = 5000 |
这里一般不怎么涉及到相机的外参(假定为单位矩阵),因为相机的外参描述的是相机坐标系和世界坐标系之间的转换关系,这通常在虚拟角色和UE4里渲染场景相融合时才会用到。
有了相机的内参后,我们就可以将关节点的位置从相机坐标系变换到图像坐标系中。不妨先将三维 SMPL 人体基模版关节点投影到一张分辨率为 256x256 的图片中:
root_transl = [0.0, 0.0, 50] # 根结点位移(不是位置) |
需要说明的是:SMPL 模型一开始就假定人体是位于相机前方正中央的。但是在很多实际的场景中,人体位置复杂多变,因此就需要一个三维变量 translation 来描述与原始假定位置的偏移。 在上面代码中,我们依然设置人体位于相机的正前方,只不过远离了相机 50 个单元的距离,然后将三维人体关节点投影到图像中得到:
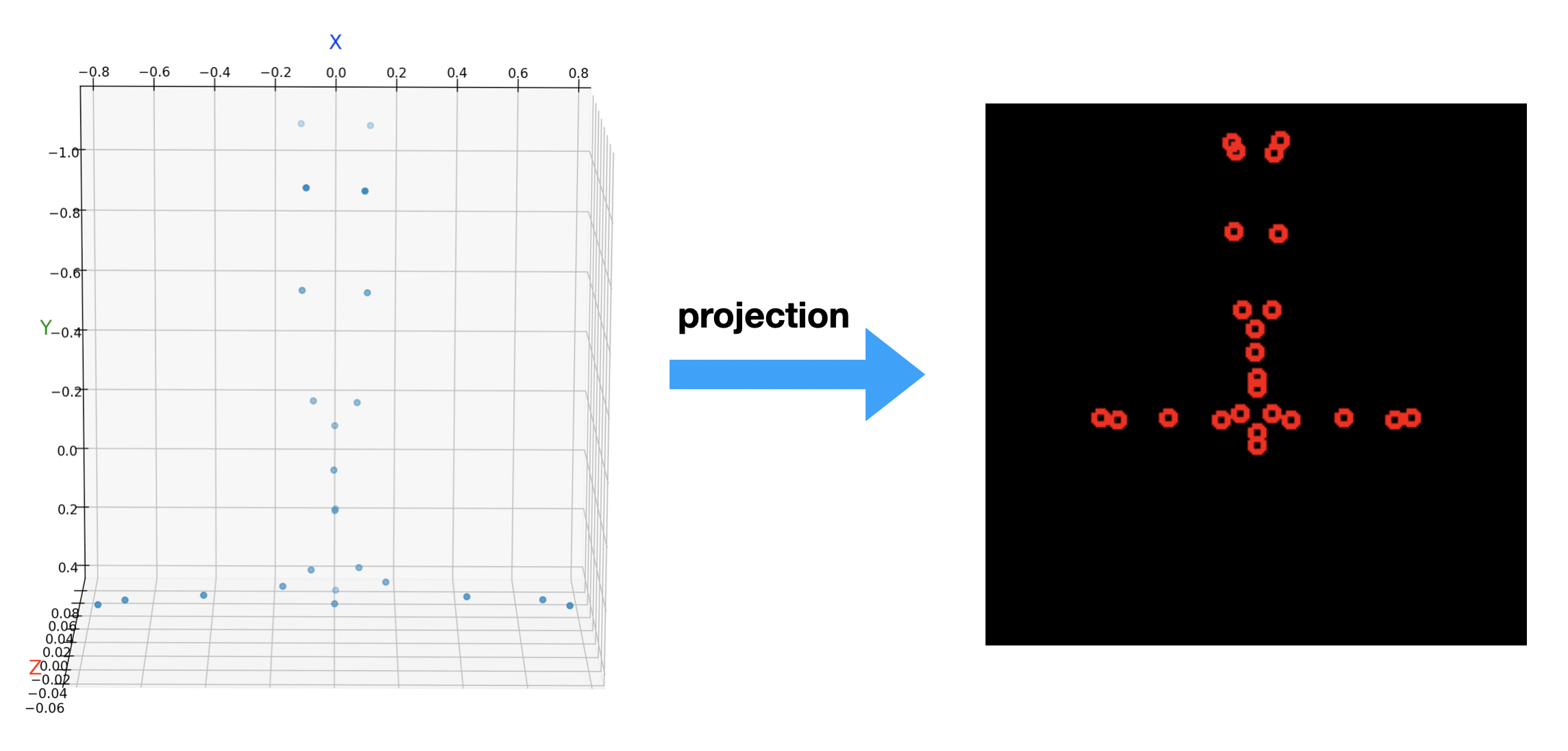
为什么人体是倒立的呢?你要知道在相机坐标系中:向前是 z 轴,向下是 y 轴,向右是 x 轴,所以基模版的关节点这么看它就是倒立了。假如你要把它变换到我们常见的世界坐标系(向前 x 轴,向右 y 轴,向上 z 轴)中,那么将它们再乘以一个相应的 transform 矩阵就行了。