老生常谈 Focal Loss —— 解决正负样本不均衡问题
最近看的一些 anchor-free 目标检测算法都普遍用到了 Focal Loss,今天就来老生常谈重新聊聊它吧!
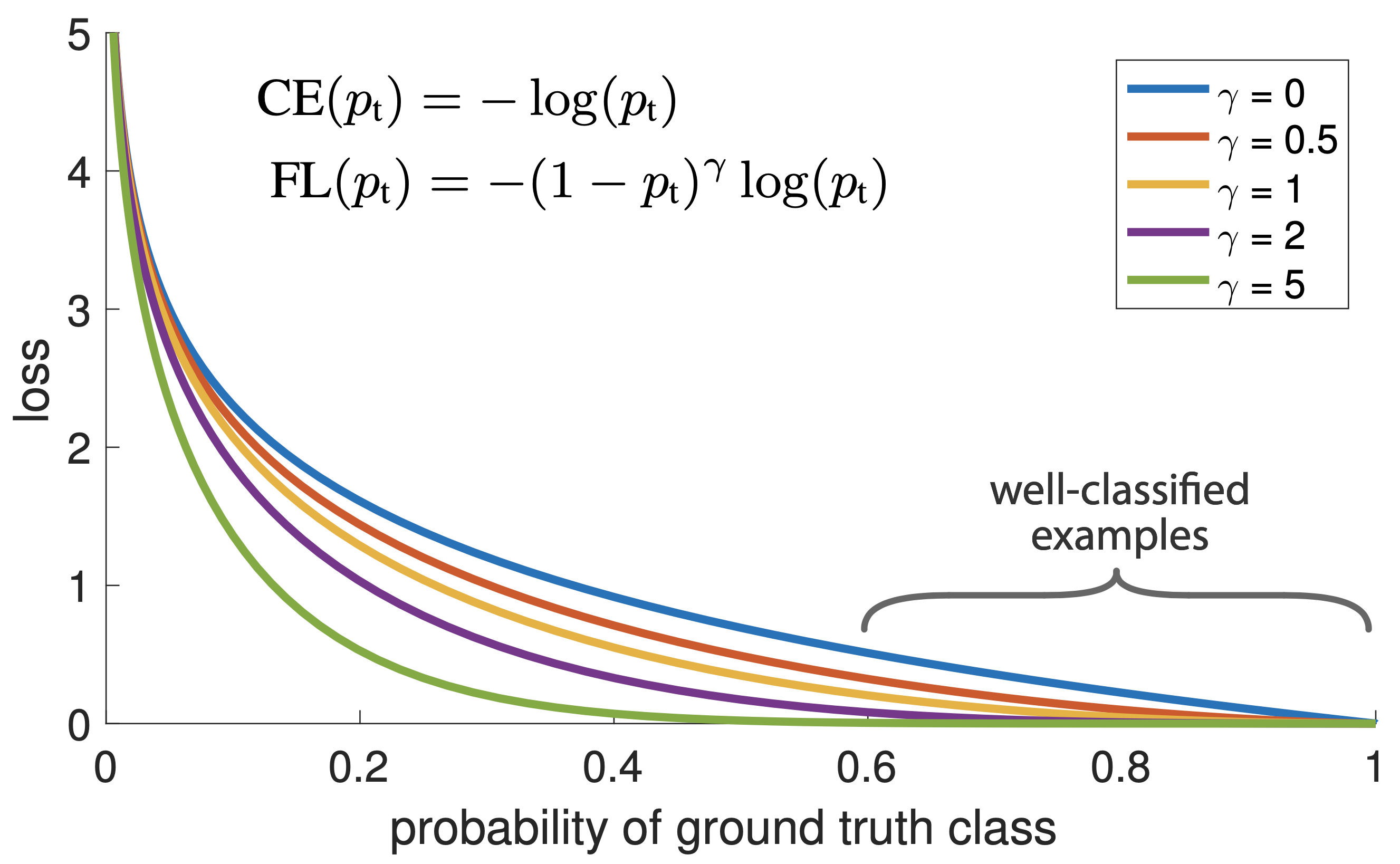
在讲 Focal Loss 之前,咱们先简单回顾一下交叉熵损失(cross entropy loss)函数。
1. 交叉熵损失
在物理学中,“熵”被用来表示热力学系统所呈现的无序程度。香农将这一概念引入信息论领域,提出了“信息熵”概念,通过对数函数来测量信息的不确定性。
交叉熵(cross entropy)是信息论中的重要概念,主要用来度量两个概率分布间的差异。假定 𝑝 和 𝑞 是数据 𝑥 的两个概率分布,通过 𝑞 来表示 𝑝 的交叉熵可如下计算:
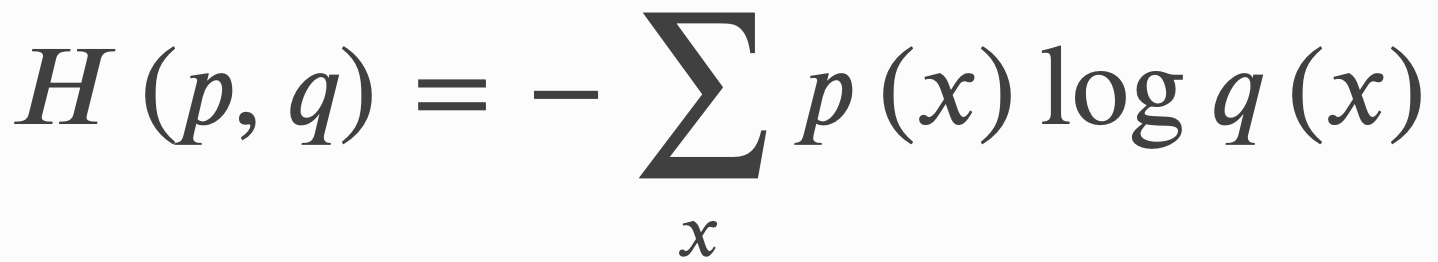
交叉熵刻画了两个概率分布 𝑝 和 𝑞 之间的距离。根据公式不难理解,如果交叉熵越小,那么两个概率分布 𝑝 和 𝑞 越接近。

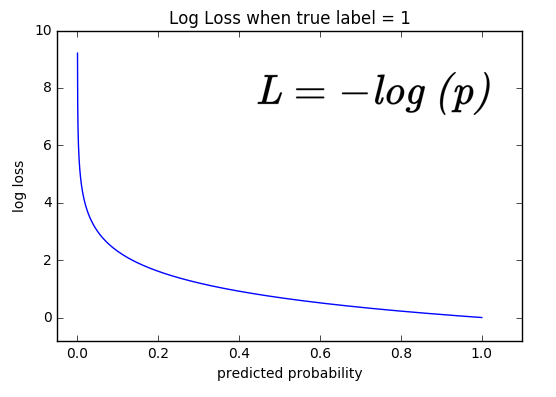
如上图所示,在神经网络中,我们通常是利用 softmax 层输出一个多分类的预测概率分布,然后与真实概率分布计算交叉熵损失。在上面公式中,通常我们是假设 𝑝 为真实概率分布, 𝑞 为预测概率分布。以一个二分类为例, 𝑝 = [1, 0],𝑞 = [ p, 1-p],那么计算出交叉熵损失为 L = - log(p)
2. Focal Loss 损失
Focal Loss 是在交叉熵损失函数上进行改进的,其背景是来源于解决 one-stage detector 里 anchor 正负样本不均衡问题。作者认为 one-stage detector 检测还不够准的原因完全在于:
- 正负样本非常不均衡,而且绝大多数负样本都是 easy example;
- 虽然这些 easy example 的损失可能比较低,但是它们数量众多,依旧对 loss 有很大贡献,从而使得梯度被 easy example 主导。
因此我们就自然想到提高困难样本的权重和降低简单样本的权重,因此在交叉熵损失函数的基础上增加一个调节因子,得到 Focal Loss 如下:
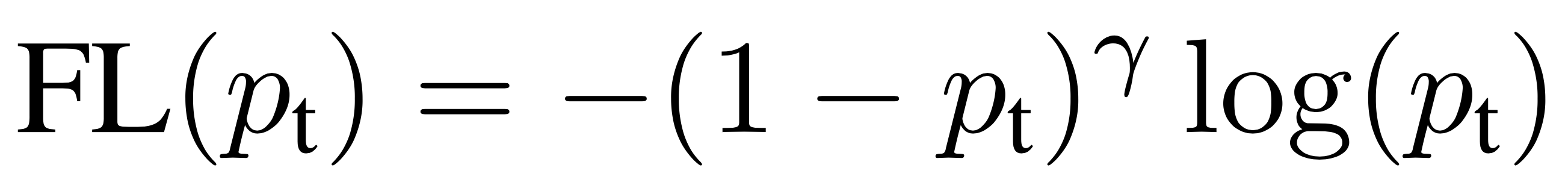
其中 γ ∈ [0, 5] 范围内。文章认为 detector 对某目标的预测概率越接近 1,那么说明这个目标就越容易被分类,属于简单样本类型。从最上面的图中可以看出:当一个样本被错误分类时它的概率 Pt 就会很低,属于困难样本,这个时候权重值就接近于 1;而当它的概率接近于 1 时,属于简单样本,其权重就会趋于 0.