DeepSort:多目标跟踪算法 Sort 的进化版
在之前的 Sort 算法中讲到:尽管 Sort 具有速度快和计算量较小的优点,但它在关联匹配时没有用到物体的表观特征,导致物体被遮挡时容易出现 id-switch 的情况。针对这个算法的痛点,原 author 团队又发明了 Sort 的进化版 —— DeepSort: Simple Online and Realtime Tracking with a Deep Associate Metric

1. 卡尔曼滤波追踪器
DeepSort 的 KalmanFilter 假定跟踪场景是定义在 8 维状态空间(u, v, γ, h, ẋ, ẏ, γ̇, ḣ)中, 边框中心(u, v),宽高比 γ,高度 h 和和它们各自在图像坐标系中的速度。这里依旧使用的是匀速运动模型,并把(u,v,γ,h)作为对象状态的直接观测量(direct observations of the object state.)。在目标跟踪中,需要估计目标的以下两个状态:
- 均值(Mean):包含目标的中心位置和速度信息,由 8 维向量(u, v, γ, h, ẋ, ẏ, γ̇, ḣ)表示,其中每个速度值初始化为 0。均值 Mean 可以通过观测矩阵 H 投影到测量空间输出(u,v,γ,h)。
- 协方差(Covariance):表示估计状态的不确定性,由 8x8 的对角矩阵表示,矩阵中数字越大则表明不确定性越大。
关于以下公式的变量和符号说明,请参考卡尔曼滤波算法,永远滴神!
1.1 predict 阶段
- step1:首先利用上一时刻 k-1 的后验估计值通过状态转移矩阵 F 变换得到当前时刻 k 的先验估计状态
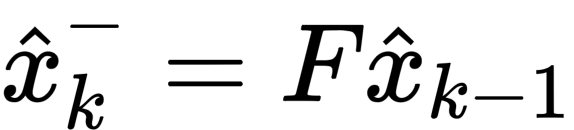

- step2:然后使用上一时刻 k-1 的后验估计协方差来计算当前时刻 k 的先验估计协方差
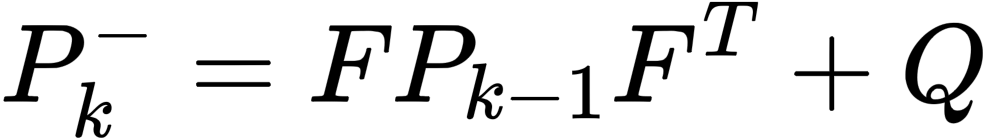
整个过程如下:
def predict(self, mean, covariance): |
predict 函数的输入为卡尔曼滤波器在上一时刻的后验估计均值 x_{k-1} 和协方差 P_{k-1},输出为当前时刻的先验估计均值x_{k} 和协方差 P_{k}。
1.2 update 阶段
- step1:首先利用先验估计协方差矩阵 P 和观测矩阵 H 以及测量状态协方差矩阵 R 计算出卡尔曼增益矩阵 K

- step2:然后将卡尔曼滤波器的先验估计值 x 通过观测矩阵 H 投影到测量空间,并计算出与测量值 z 的残差 y
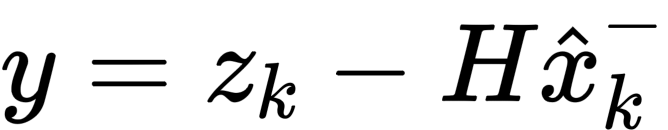
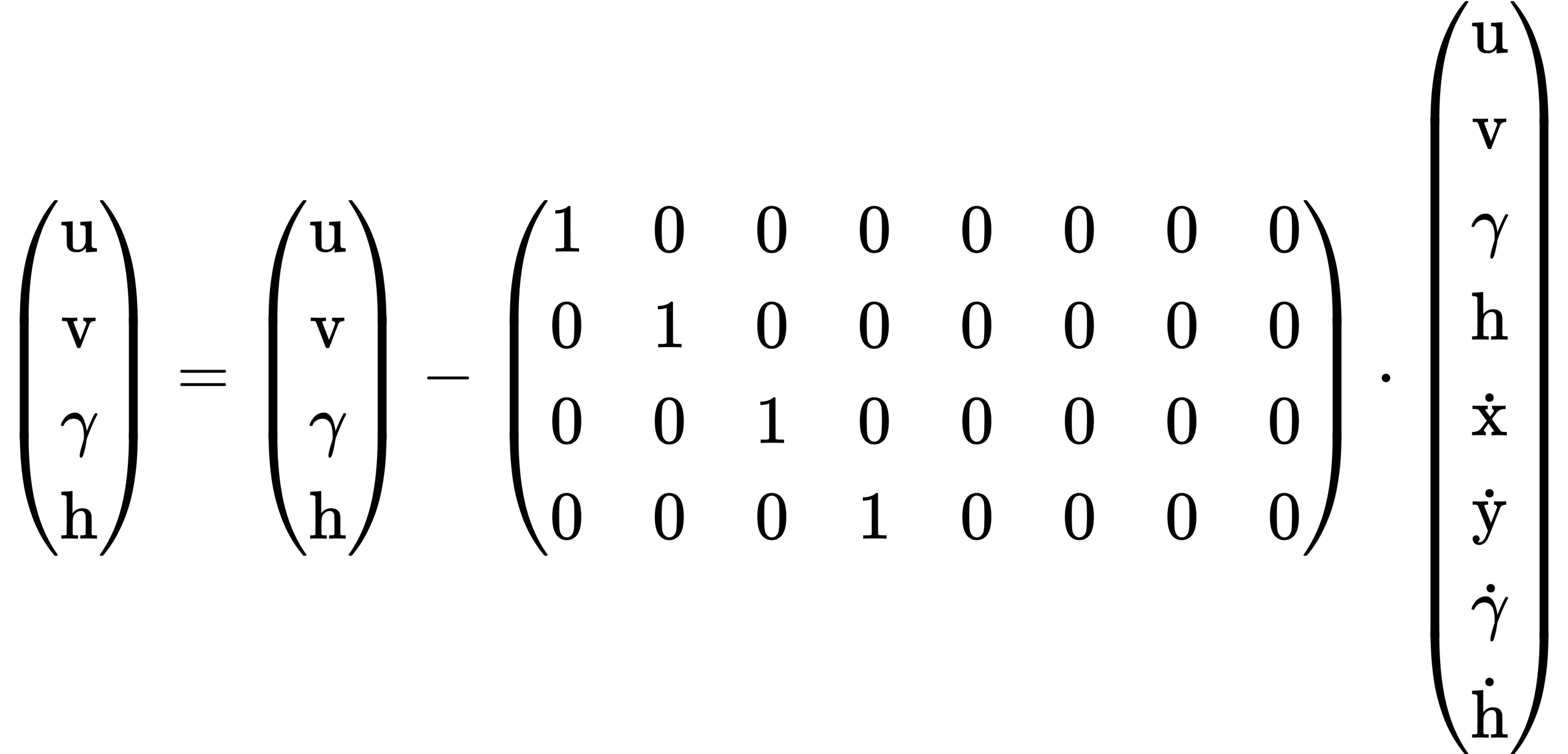
- step3:将卡尔曼滤波器的预测值和测量值按照卡尔曼增益的比例相融合,得到后验估计值 x
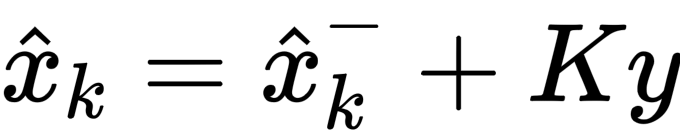
- step4:计算出卡尔曼滤波器的后验估计协方差
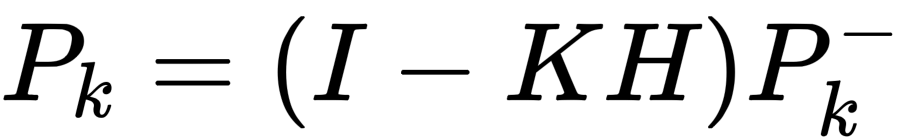
整个过程如下:
def update(self, mean, covariance, measurement): |
| 最后总结一下:predict 阶段和 update 阶段都是为了计算出卡尔曼滤波的估计均值 x 和协方差 P,不同的是前者是基于上一历史状态做出的先验估计,而后者则是融合了测量值信息并作出校正的后验估计。 |
1.3 跟踪器的状态
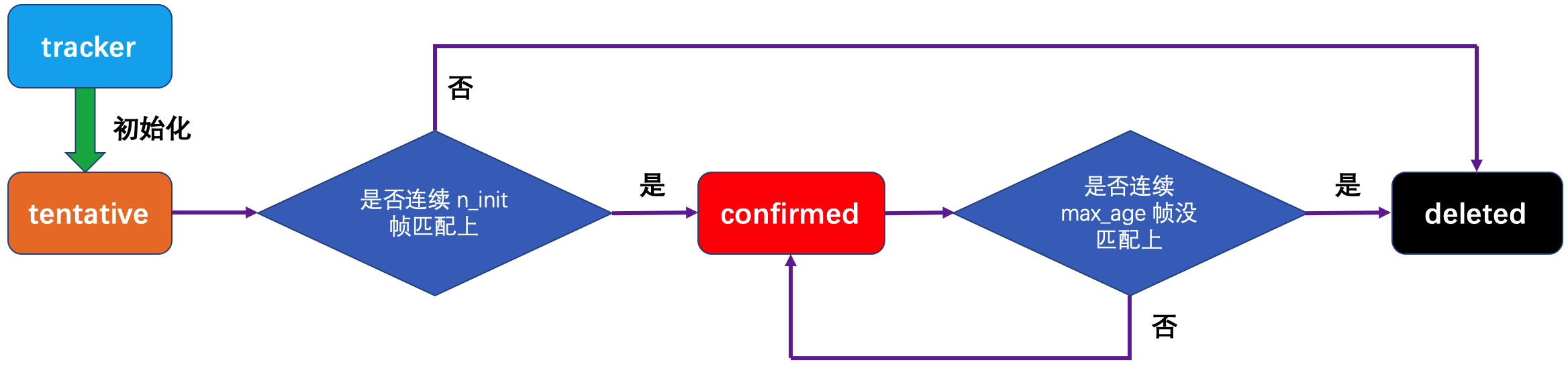
DeepSort 的跟踪器一共有 3 种状态:当 tracker 初始化时,分配为待定状态(tentative);如果连续 n_init 帧匹配上,则转化为确定状态(confirmed),否则为删除状态(deleted);如果 tracker 在确定状态下连续 max_age 帧没匹配上,那么就会变成删除状态被回收。
2. 关联度量
解决卡尔曼滤波器的预测状态和测量状态之间的关联可以通过构建匈牙利匹配来实现,在这个过程中需要结合两个合适的指标来整合物体的运动信息和外观特征。
2.1 马氏距离
为了整合物体的运动信息,使用了预测状态和测量状态之间的(平方)马氏距离:
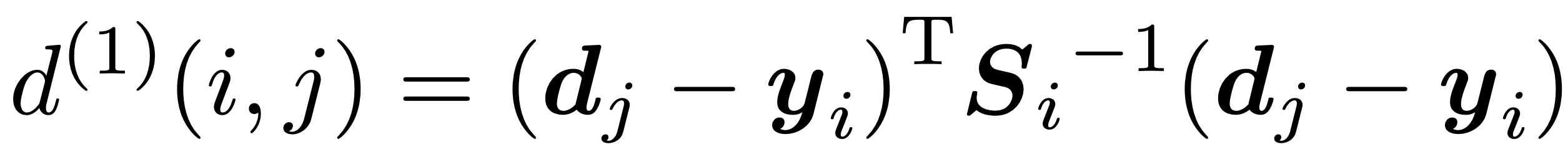
在上式中,d 和 y 分别代表测量分布和预测分布,S 为两个分布之间的协方差矩阵。由于测量分布的维度(4 维)和预测分布的维度(8 维)不一致,因此需要先将预测分布通过观测矩阵 H 投影到测量空间中(这一步其实就是从 8 个估计状态变量中取出前 4 个测量状态变量,详见 project 函数)。
# Project state distribution to measurement space. |
协方差矩阵 S 是一个实对称正定矩阵,可以使用 Cholesky 分解来求解马氏距离,这部分内容就不展开讨论。在 DeepSort 代码中,计算马氏距离的整个过程如下:
# Compute gating distance between state distribution and measurements. |
马氏距离通过计算检测框距离预测框有多远的偏差来估计跟踪器状态的不确定性,此外还可以通过在 95% 的置信区间上从逆 χ2 分布中计算出的马氏距离来排除不可能的关联。在 DeepSort 的 4 维测量空间中,相应的马氏距离阈值为 9.4877,如果两个匹配框之间的马氏距离大于这个值,那么就认为两个框是不可能关联了。
2.2 外观特征
当物体运动状态的不确定性比较低时,使用马氏距离确实是一个不错的选择。由于卡尔曼滤波器使用的是匀速运动模型,它只能对物体的运动位置提供一个相对粗略的线性估计。当物体突然加速或减速时,跟踪器的预测框和检测框之间的距离就会变得比较远,这时仅使用马氏距离就会变得非常不准确。
因此 DeepSort 还对每个目标设计了一个深度外观特征描述符,它其实是一个在行人重识别数据集上离线训练的 ReID 网络提取到的 128 维单位特征向量(模长为 1 )。对于每个追踪器 tracker,保留它最后 100 个与检测框关联成功的外观特征描述符集合 R 并计算出它们和检测框的最小余弦距离:
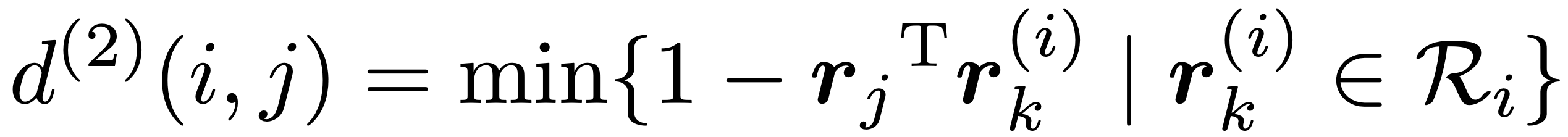
同样,可以设置一个合适的阈值来排除那些外观特征相差特别大的匹配。
2.3 互相补充
上述两个指标可以互相补充从而解决关联匹配的不同问题:一方面,马氏距离基于运动可以提供有关可能的物体位置的信息,这对于短期预测特别有用;另一方面,当运动的判别力较弱时,余弦距离会考虑外观信息,这对于长时间遮挡后恢复身份特别有用。
为了建立关联问题,我们使用加权总和将两个指标结合起来:
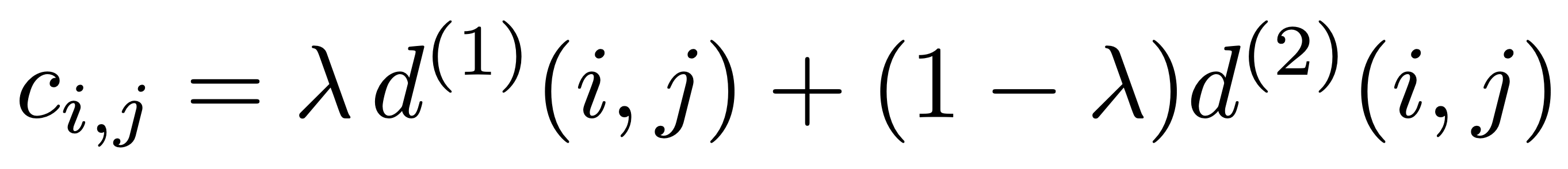
如果它同时在两个指标的门控范围之内,我们称其为可接受的关联。可以通过超参数 λ 来控制每个指标对合并成本的影响。在论文的实验过程中,发现当摄像机运动较大时,将 λ=0 是合理的选择(此时仅用到了外观信息)。
3.1 匹配问题
3.1 级联匹配
为了解决全局分配问题中检测框与跟踪器的关联,我们引入了一个级联来解决一系列的子问题。不妨先考虑这种场景:当物体被长时间遮挡时,后续的卡尔曼滤波预测结果会增大与物体位置关联的不确定性。因此概率分布会在状态空间中弥散,观察似然性就会变得比较平坦。关联度量应该增加检测框到预测框之间的距离来考虑这种概率分布的弥散,故而引入了一个级联匹配来优先考虑年龄较小的跟踪器:
def matching_cascade( |
在级联匹配的花费矩阵里,元素值为马氏距离和余弦距离的加权和。该匹配的精髓在于:挑选出所有 confirmed tracks,优先让那些年龄较小的 tracks 和未匹配的检测框相匹配,然后才轮得上那些年龄较大的 tracks 。这就使得在相同的外观特征和马氏距离的情况下,年龄较小的跟踪器更容易匹配上。至于年龄 age 的定义,跟踪器每次 predict 时则 age + 1。
3.2 IOU 匹配
这个阶段是发生在级联匹配之后,匹配的跟踪器对象为那些 unconfirmed tracks 以及上一轮级联匹配失败中 age 为 1 的 tracks. 这有助于解决因上一帧部分遮挡而引起的突然出现的外观变化,从而减少被遗漏的概率。
# 从所有的跟踪器里挑选出 unconfirmed tracks |