随手用 Python 撸一个单目视觉里程计的例子

最近因工作需要，开始接触到一些关于 SLAM（Simultaneous Localization and Mapping）的研究。网上关于 slam 的资料有很多，譬如高博的十四讲，github 上的 VINS 等等。但是他们大多是用 C++ 写的，并且环境依赖复杂。今天， 我使用 Python 手撸了一个简单的单目 slam，对 slam 有了一个初步的认识。完整的代码在这里。

1. ORB 特征点检测

ORB 特征由关键点和描述子两部分组成，它的关键点称为 “Oriented FAST”，是一种改进的 FAST 角点，而描述子则称为 BRIEF。在 OpenCV 中，我们可以这样：

orb = cv2.ORB_create()
image = cv2.cvtColor(frame.image, cv2.COLOR_BGR2GRAY)
# detection corners
pts = cv2.goodFeaturesToTrack(image, 3000, qualityLevel=0.01, minDistance=3)
# extract features
kps = [cv2.KeyPoint(x=pt[0][0], y=pt[0][1], _size=20) for pt in pts]
kps, des = orb.compute(image, kps)

我们首先需要将图片转成灰度图， 然后利用 goodFeaturesToTrack 找出图片中的高质量的角点， 接着使用 orb 里的 compuete 函数计算出这些角点的特征：它会返回 kps 和 des，kps 给出了角点在图像中坐标，而 des 则是这些角点的描述子，一般为 32 维的特征向量。

frame 1: kps[0]=(294.0, 217.0), des[0]=[ 66 245  18 ...  39 206]

2. 特征点匹配

特征点匹配的意思就是将本帧检测的所有角点和上一帧的角点进行匹配，因此需要将上一帧的角点 last_kps 和描述子 last_des 存储起来。此外还需要 idx 记录每帧的序列号，并且从第二帧才开始做匹配。我们构造了一个 Frame 类，并将它们定义为类的属性，在实例初始化的时候再将这些属性传递给对象。

class Frame(object):
    idx = 0
    last_kps, last_des, last_pose = None, None, None

    def __init__(self, image):
        """
        只要一经初始化，Frame 就会把上一帧的信息传递给下一帧
        """
        Frame.idx += 1

        self.image = image
        self.idx   = Frame.idx
        self.last_kps  = Frame.last_kps
        self.last_des  = Frame.last_des
        self.last_pose = Frame.last_pose

我直接使用了暴力匹配（Brute-Force）的方法对两帧图片的角点进行配准，通过 cv2.BFMatcher 可以创建一个匹配器 bfmatch，它有两个可选的参数：

• normType：度量两个角点之间距离的方式，由于 ORB 是一种基于二进制字符串的描述符，因此可以选择汉明距离 (cv2.NORM_HAMMING)。
• crossCheck：为布尔变量，默认值为 False。如果设置为 True，匹配条件就会更加严格，只有当两个特征点互相为最佳匹配时才可以。

使用 knnMatch() 可以为每个关键点返回 k 个最佳匹配（将序排列之后取前 k 个），其中 k 是用户自己设定的，这里设置成 k=2。

bfmatch = cv2.BFMatcher(cv2.NORM_HAMMING)
matches = bfmatch.knnMatch(frame.curr_des, frame.last_des, k=2)

将 frame.curr_des 、 frame.last_des 和 matches 的数量打印出来：

frame: 16, curr_des: 1660, last_des: 1597, matches: 1660
frame: 17, curr_des: 1484, last_des: 1660, matches: 1484

我们发现 matches 的数量始终与 frame.curr_des 相等，这是因为这里是从上一帧 frame.last_des 给当前帧 frame.curr_des 找最佳匹配点，并且每个 match 返回的是 2 个 DMatch 对象，它们具有以下属性：

• DMatch.distance ：关键点之间的距离，越小越好。
• DMatch.trainIdx ：目标图像中描述符的索引。
• DMatch.queryIdx ：查询图像中描述符的索引。
• DMatch.imgIdx：目标图像的索引。

如果第一名的距离小于第二名距离的 75%，那么将认为第一名大概率是匹配上了，此时 m.queryIdx 为当前帧关键点的索引，m.trainIdx 为上一帧关键点的索引，match_kps 返回的是每对配准点的位置。

for m,n in matches:
    if m.distance < 0.75*n.distance:
        idx1.append(m.queryIdx)
        idx2.append(m.trainIdx)

        p1 = frame.curr_kps[m.queryIdx]     # 当前帧配准的角点位置
        p2 = frame.last_kps[m.trainIdx]     # 上一帧配置的角点位置
        match_kps.append((p1, p2))

在下图中：红色的是当前帧的关键点，蓝色的是当前帧关键点的位置与上一帧关键点位置的连线。由于 🚗 是向前行驶，因此关键点相对 🚗 是往后运动的。

for kp1, kp2 in zip(frame.curr_kps, frame.last_kps):
    u1, v1 = int(kp1[0]), int(kp1[1])
    u2, v2 = int(kp2[0]), int(kp2[1])
    
    # 用圆圈画出当前帧角点的位置
    cv2.circle(frame.image, (u1, v1), color=(0,0,255), radius=3)
    # 用直线追踪角点的行动轨迹
    cv2.line(frame.image, (u1, v1), (u2, v2), color=(255,0,0))

3. RANSAC 去噪和本质矩阵

RANSAC (RAndom SAmple Consensus, 随机采样一致) 算法是从一组含有 “外点” (outliers) 的数据中正确估计数学模型参数的迭代算法。RANSAC 算法有 2 个基本的假设：

• 假设数据是由“内点”和“外点”组成的。“内点”就是组成模型参数的数据，“外点”就是不适合模型的异常值，通常是那些估计曲线以外的离群点。
• 假设在给定一组含有少部分“内点”的数据中，存在一个模型可以估计出符合“内点”变化的规律。

具体的细节这里不再展开，感兴趣的话可以看这里，这里是直接使用三方库里的 scikit-image 里的 ransac 算法进行求解。由于我们在求解本质矩阵的时候，需要利用相机内参将角点的像素坐标进行归一化：

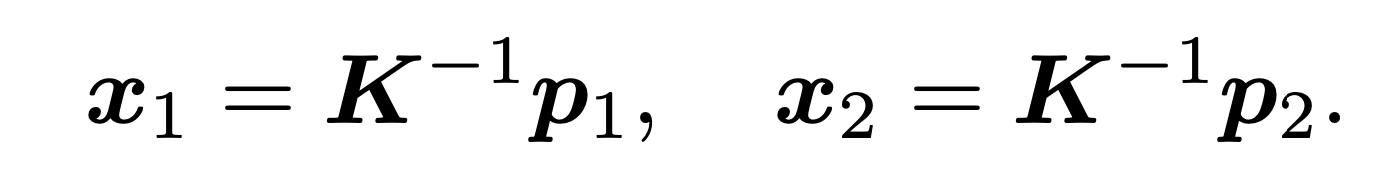
其中 p1 和 p2 分别为配对角点在图片上的像素位置，那么归一化的代码如下：

def normalize(pts):
    Kinv = np.linalg.inv(K)
    # turn [[x,y]] -> [[x,y,1]]
    add_ones = lambda x: np.concatenate([x, np.ones((x.shape[0], 1))], axis=1)
    norm_pts = np.dot(Kinv, add_ones(pts).T).T[:, 0:2]
    return norm_pts

slam 知识里给出了本质矩阵和归一化坐标之间的关系，它可以用一个简洁的公式来表达：

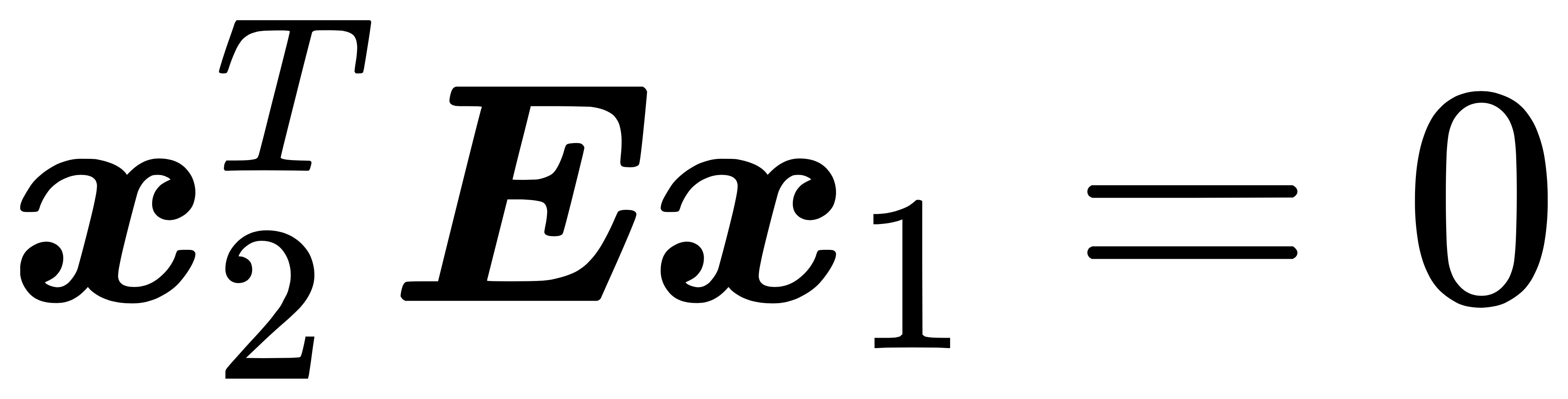
其中本质矩阵 E 是平移向量 t 和旋转矩阵 R 的外积：

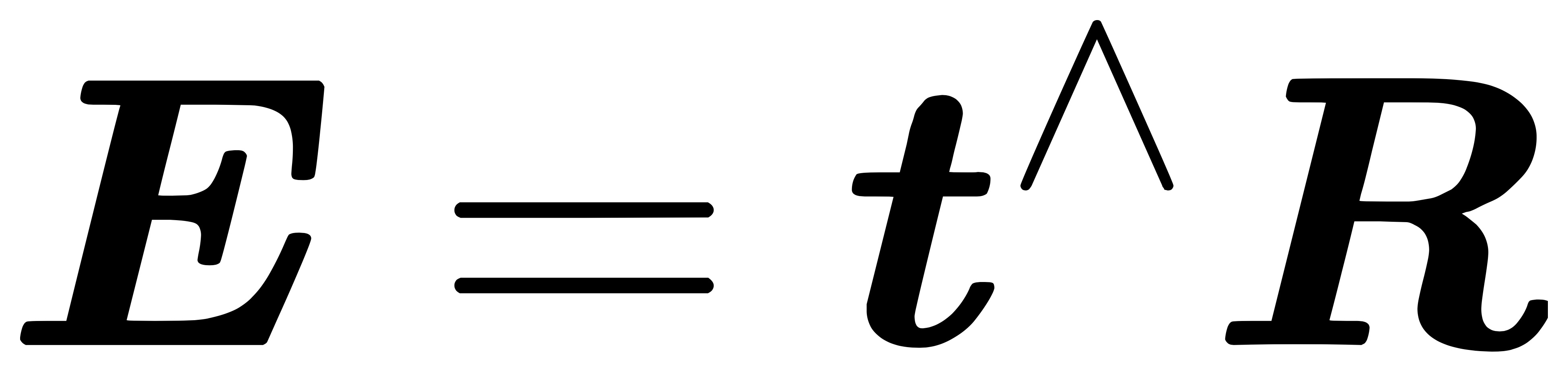
本质矩阵 E 是一个 3x3 的矩阵，有 9 个未知元素。然而，上面的公式中 x 使用的是齐次坐标（已经有一个已知的 1）。而齐次坐标在相差一个常数因子下是相等，因此在单位尺度下只需 8 个点即可求解。

def fit_essential_matrix(match_kps):
    match_kps = np.array(match_kps)

    # 使用相机内参对角点坐标归一化
    norm_curr_kps = normalize(match_kps[:, 0])
    norm_last_kps = normalize(match_kps[:, 1])

    # 求解本质矩阵和内点数据
    model, inliers = ransac((norm_curr_kps, norm_last_kps),
                            EssentialMatrixTransform,
                            min_samples=8,              # 最少需要 8 个点
                            residual_threshold=0.005,
                            max_trials=200)

    frame.curr_kps = frame.curr_kps[inliers]   # 保留当前帧的内点数据
    frame.last_kps = frame.last_kps[inliers]   # 保留上一帧的内点数据

    return model.params       # 返回本质矩阵

可以看到，经过 RANSAC 去燥后，噪点数据消失了很多，角点的追踪情况基本稳定。但是经过筛选后，角点的数量只有原来的三分之一左右了。

frame: 46, curr_des: 1555, last_des: 1467, match_kps: 549
---------------- Essential Matrix ----------------
[[-2.86637732e-04 -1.16930419e+00  1.12798916e-01]
 [ 1.16673848e+00 -2.40819717e-03 -2.60028204e-01]
 [-1.10221539e-01  2.67480554e-01 -1.20159639e-03]]

4. 本质矩阵分解

接下来的问题是如何根据已经估计得到的本质矩阵 E，恢复出相机的运动 R，t。这个过程是由奇异值分解得到的：

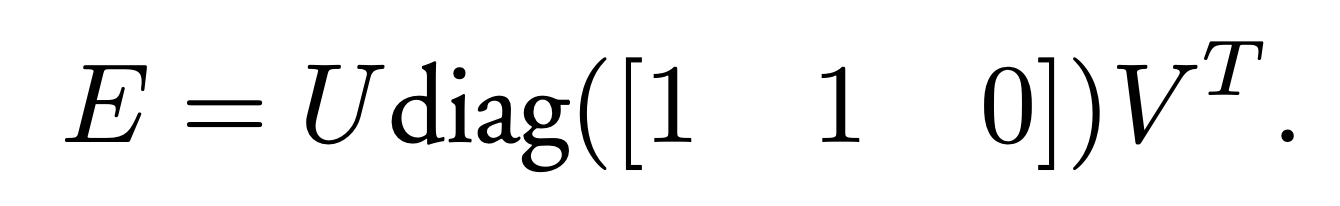
我们发现对角矩阵 diag([1, 1, 0]) 可以由 Z 和 W 拆分得到。

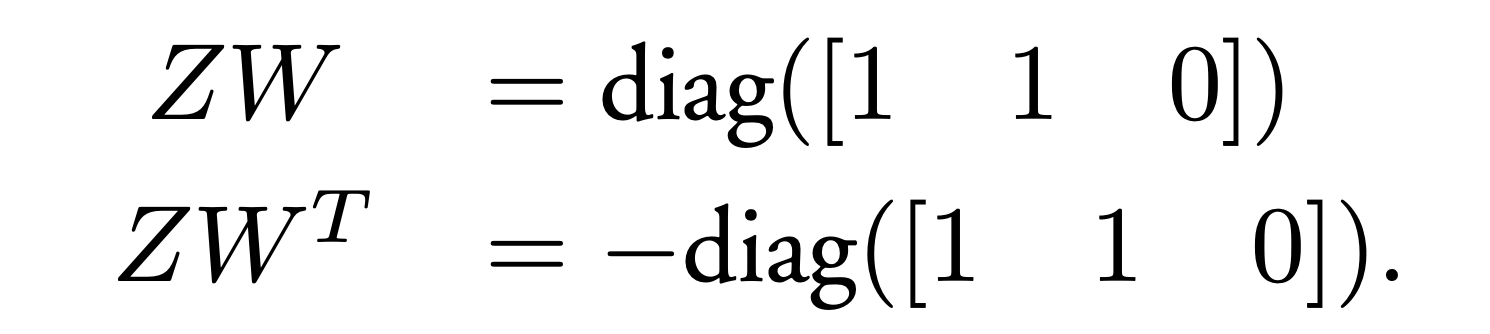
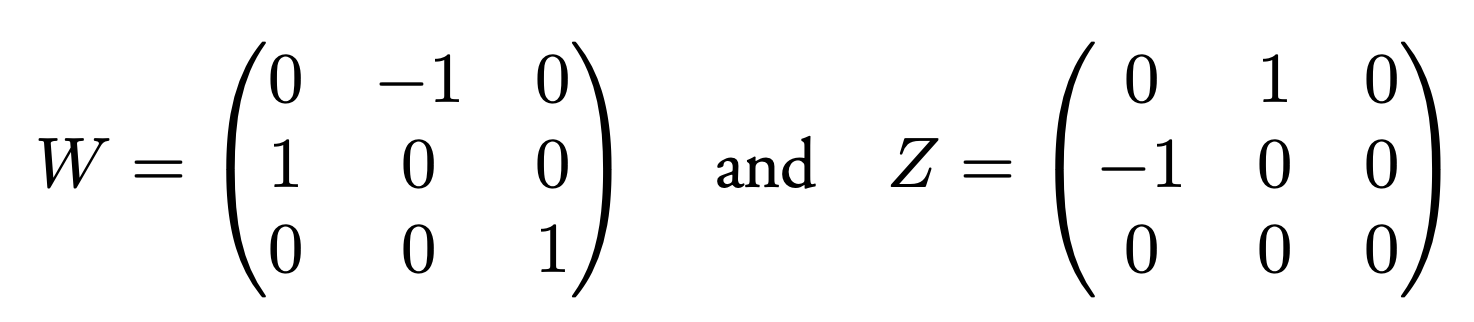
将 Z 和 W 代入进来，令 E = S R。可以分解成两种情况：

• 情况 1:

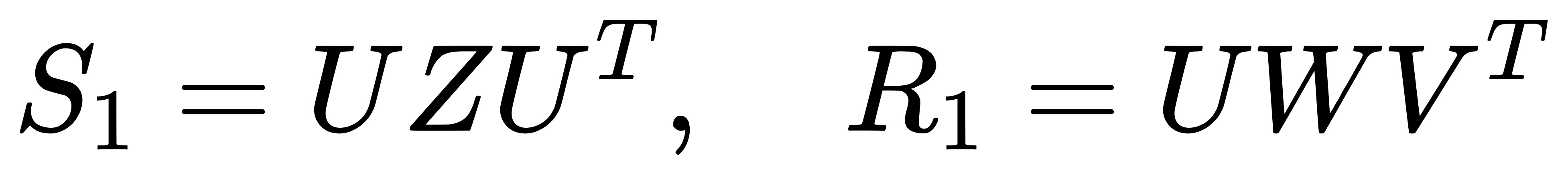
• 情况 2:

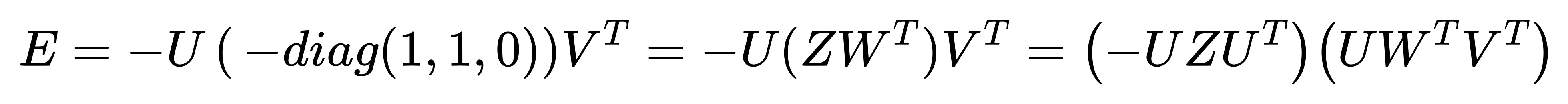
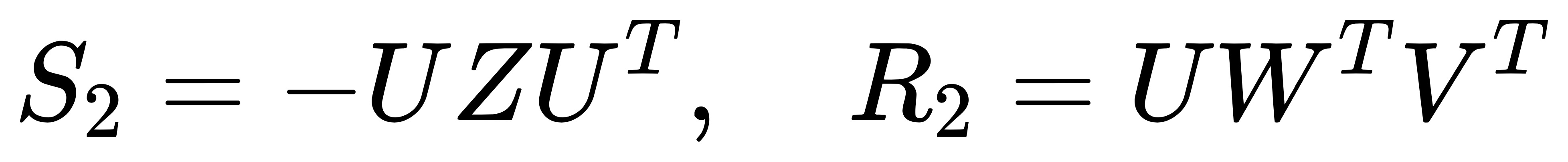
我们发现，此时已经将旋转矩阵 R 分离出来了，它有两种情况：分别等于 R1 和 R2。接下来我们需要考虑平移向量 t，可以证明出 t 其实是在 S 的零向量空间里，因为：

结合线性代数的知识，不难求出 t = U * (0, 0, 1) = u3 (即 U 的最后一列)。考虑到给 t 乘以一个非零尺度因子 λ， 对于 E 而言这种情况依旧有效，而对于 t 而言， 当 λ = ± 1 时，它们物理的意义（方向）却是不同的。综上，在已知第一个相机矩阵 P = [ I ∣ 0 ] 的情况下，第二个相机矩阵 P′ 有如下 4 种可能的解：

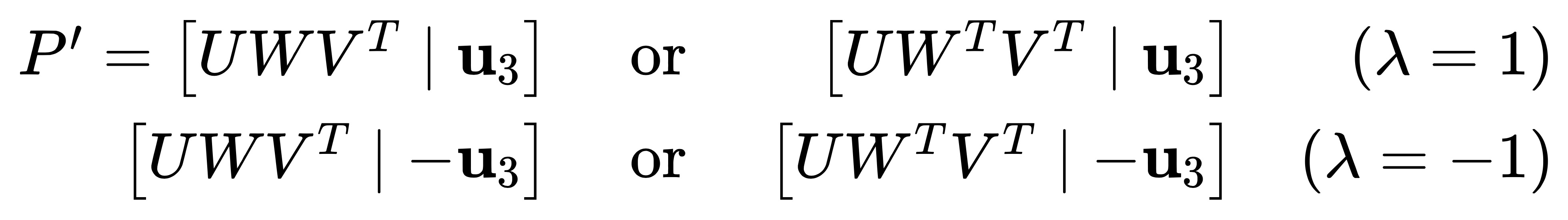
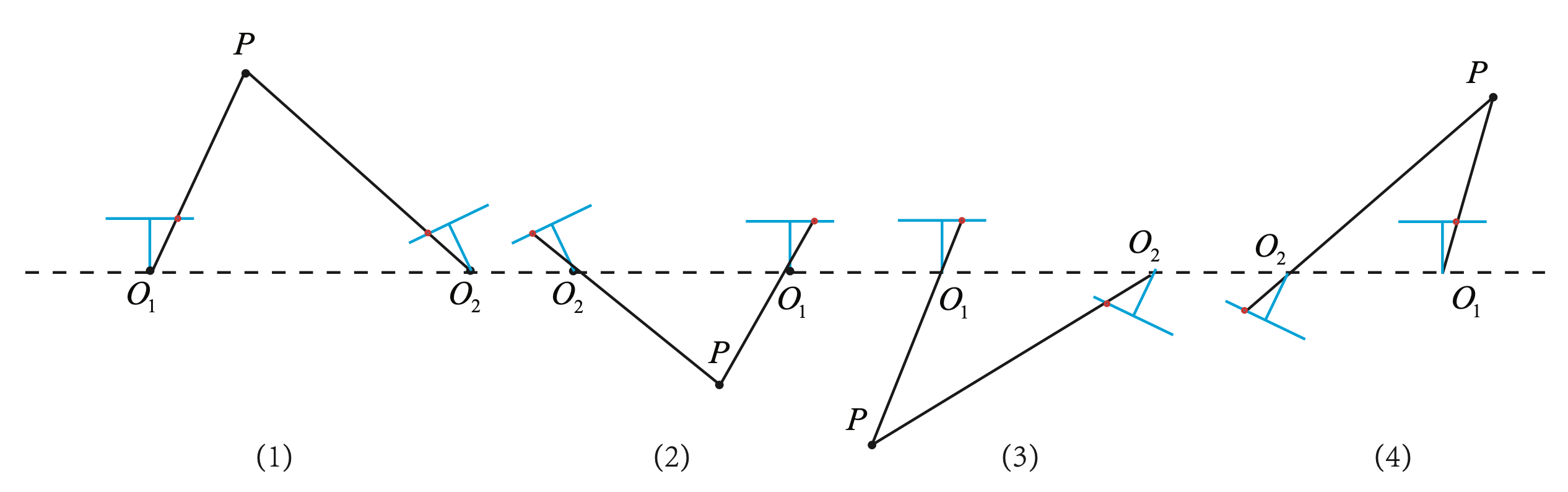
我们发现上面 4 种解其实是 2 种 R 和 2 种 t 之间的排列组合，只有当点 P 位于两个相机前方时才具有正深度，即 (1) 才是唯一正确解。

OpenCV 提供了从本质矩阵中恢复相机的 Rt 的方法：

void cv::decomposeEssentialMat( InputArray _E, OutputArray _R1, OutputArray _R2, OutputArray _t )
{
    Mat E = _E.getMat().reshape(1, 3);
	CV_Assert(E.cols == 3 && E.rows == 3);
	
    Mat D, U, Vt;
	SVD::compute(E, D, U, Vt);
	
	if (determinant(U) < 0) U *= -1.;
	if (determinant(Vt) < 0) Vt *= -1.;
	
    Mat W = (Mat_<double>(3, 3) << 0, 1, 0, -1, 0, 0, 0, 0, 1);
    W.convertTo(W, E.type());
    Mat R1, R2, t;
    
    R1 = U * W * Vt;
    R2 = U * W.t() * Vt;
    t = U.col(2) * 1.0;
    
    R1.copyTo(_R1);
    R2.copyTo(_R2);
    t.copyTo(_t);
}

可以看出 cv::decomposeEssentialMat 函数输出了 R1、R2 和 t，因此 4 种可能的解分别为：[R1,t], [R1,−t], [R2,t], [R2,−t]， ORB_SLAM2 里使用了 CheckRT 函数对它们进行判断。考虑到 demo 视频里 🚗 是一直往前行驶，且没有转弯。因此相机 t = (x, y, z) 里的 z > 0，并且相机 R 的对角矩阵将接近 diag([1, 1, 1]) ，从而我们可以直接过滤出唯一解。

def extract_Rt(E):
    W = np.mat([[0,-1,0],[1,0,0],[0,0,1]],dtype=float)
    U,d,Vt = np.linalg.svd(E)

    if np.linalg.det(U)  < 0: U  *= -1.0
    if np.linalg.det(Vt) < 0: Vt *= -1.0

    # 相机没有转弯，因此 R 的对角矩阵非常接近 diag([1,1,1])
    R = (np.dot(np.dot(U, W), Vt))
    if np.sum(R.diagonal()) < 0:
        R = np.dot(np.dot(U, W.T), Vt)

    t = U[:, 2]     # 相机一直向前，分量 t[2] > 0
    if t[2] < 0:
        t *= -1

    Rt = np.eye(4)
    Rt[:3, :3] = R
    Rt[:3, 3] = t
    return Rt          # Rt 为从相机坐标系的位姿变换到世界坐标系的位姿

由于平移向量的分量 t[2] > 0，我们很容易知道 Rt 为从相机坐标系的位姿变换到世界坐标系的位姿

5. 三角测量

下一步我们需要用相机的运动估计特征点的空间位置，在单目 SLAM 中仅通过单目图像是无法获得像素的深度信息，我们需要通过三角测量（Triangulation）的方法估计图像的深度，然后通过直接线性变化（DLT）进行求解。

假设点 P 的世界坐标为 X_{w}，图像坐标为 X_{uv}，相机的内参和位姿分别为 K 和 P_{cw}，那么得到：

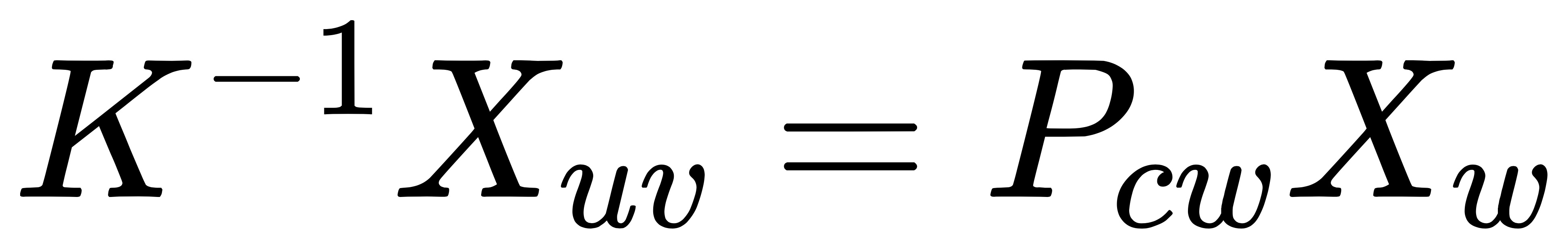
将下标去掉，使用相机内参将两个匹配的角点像素坐标进行归一化，代入到上述方程中便得到：

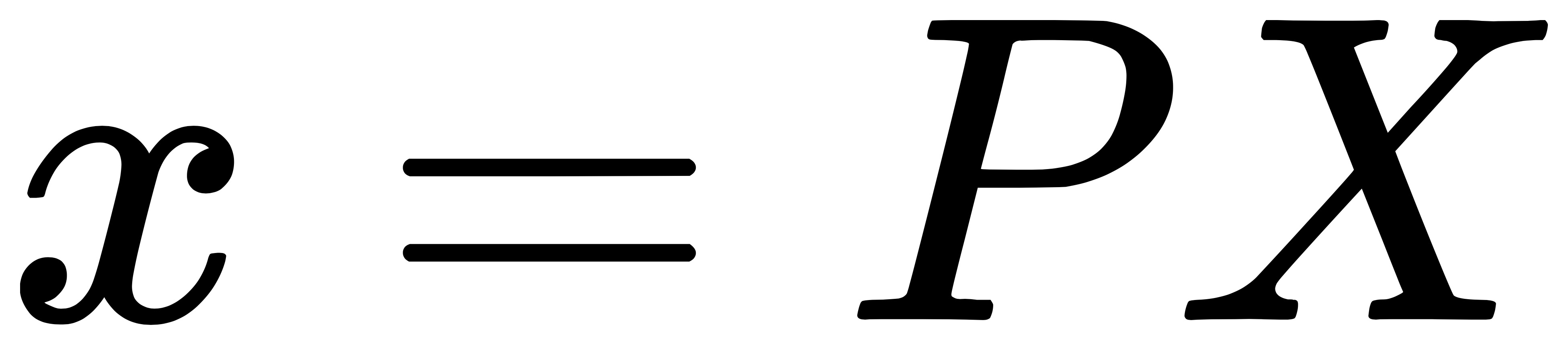
使用 DLT 的话我们对上面两个公式进行一个简单的变换，对等式两边分别做外积运算：

由于 x={u, v, 1} ，结合外积运算的知识（详见 slam 十四讲 75 页），我们便得到以下方程：

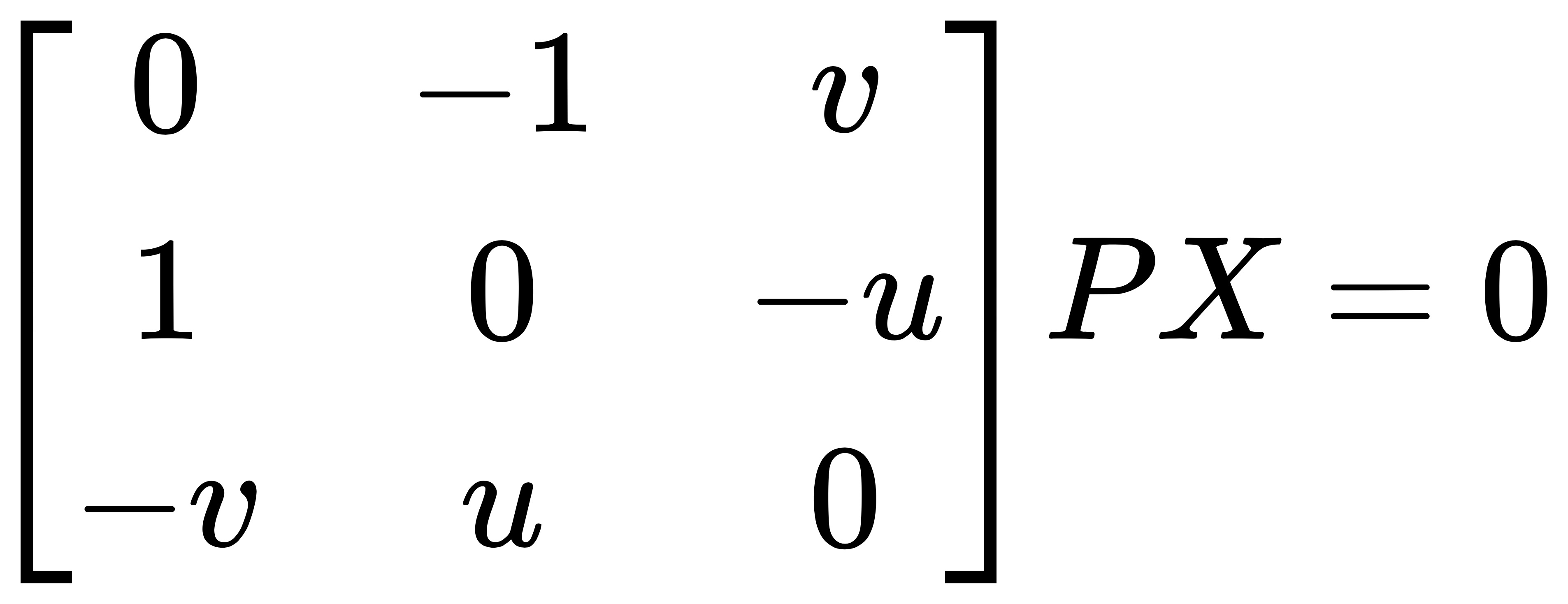
我们不妨令：

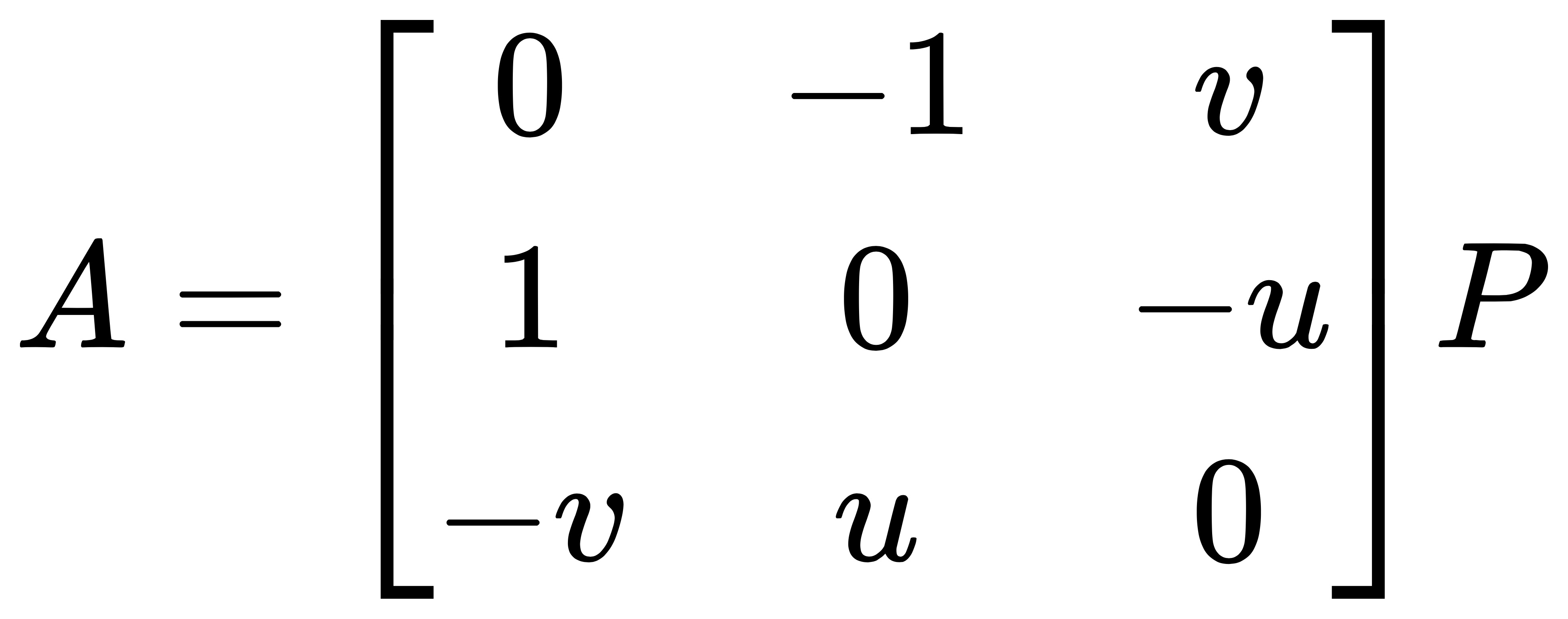
将两个匹配的角点和相机位姿代入上述方程中便得到 A：

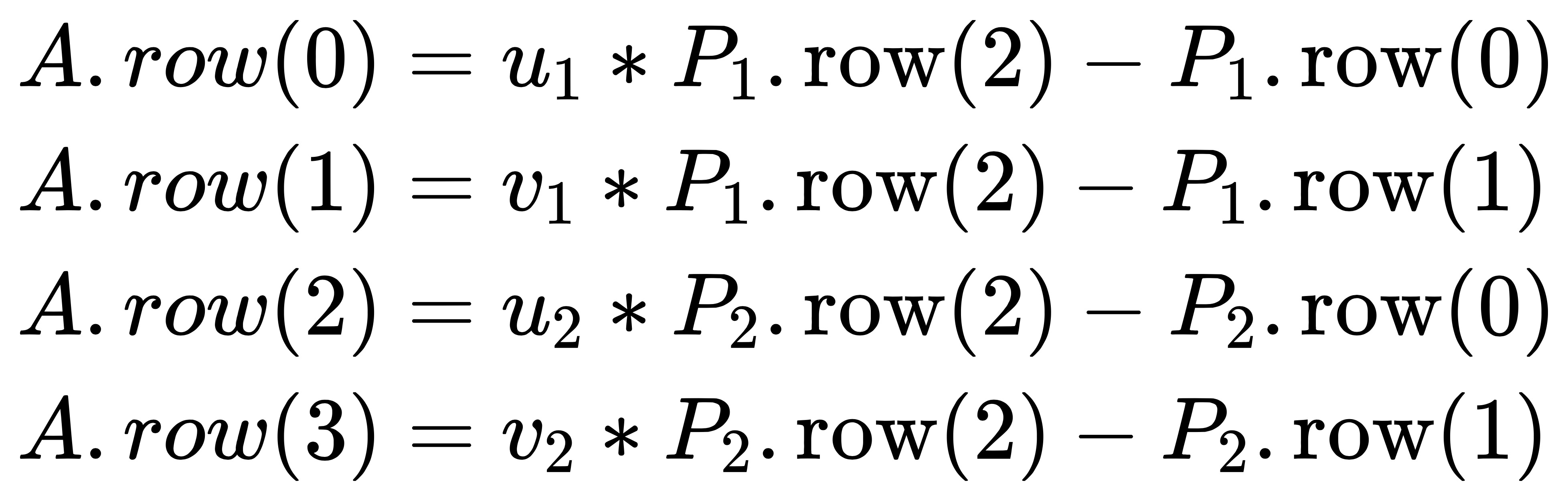
因此便可以简化成 AX=0，从而可以使用最小二乘法来求解出 X，ORB_SLAM2 中的求解过程如下：

void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
    cv::Mat A(4,4,CV_32F);

    A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
    A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
    A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
    A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);

    cv::Mat u,w,vt;
    cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
    x3D = vt.row(3).t();
    x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
}

// Camera 1 Projection Matrix K[I|0]                  # 这里假设世界坐标系为相机 1 坐标系
cv::Mat P1(3,4,CV_32F,cv::Scalar(0));
K.copyTo(P1.rowRange(0,3).colRange(0,3));

// Camera 2 Projection Matrix K[R|t]                  # 相机 2 与 相机的位姿 R，t
cv::Mat P2(3,4,CV_32F);
R.copyTo(P2.rowRange(0,3).colRange(0,3));
t.copyTo(P2.rowRange(0,3).col(3));
P2 = K*P2;

const cv::KeyPoint &kp1 = vKeys1[vMatches12[i].first];
const cv::KeyPoint &kp2 = vKeys2[vMatches12[i].second];
cv::Mat p3dC1;

Triangulate(kp1,kp2,P1,P2,p3dC1);

如下所示，我使用了 Python 对整个三角测量的计算过程进行了复现。值得注意的是，上述的相机位姿是指从空间点 P 从世界坐标系变换到相机坐标下点变换矩阵。如果你不清楚相机位姿的概念，请看什么是相机位姿？

def triangulate(pts1, pts2, pose1, pose2):
    pose1 = np.linalg.inv(pose1)            # 从世界坐标系变换到相机坐标系的位姿, 因此取逆
    pose2 = np.linalg.inv(pose2)

    pts1 = normalize(pts1)                 # 使用相机内参对角点坐标归一化
    pts2 = normalize(pts2)

    points4d = np.zeros((pts1.shape[0], 4))
    for i, (kp1, kp2) in enumerate(zip(pts1, pts2)):
        A = np.zeros((4,4))
        A[0] = kp1[0] * pose1[2] - pose1[0]
        A[1] = kp1[1] * pose1[2] - pose1[1]
        A[2] = kp2[0] * pose2[2] - pose2[0]
        A[3] = kp2[1] * pose2[2] - pose2[1]
        _, _, vt = np.linalg.svd(A)         # 对 A 进行奇异值分解
        points4d[i] = vt[3]

    points4d /= points4d[:, 3:]            # 归一化变换成齐次坐标 [x, y, z, 1]
    return points4d

6. pipeline 流程

def process_frame(frame):
    # 提取当前帧的角点和描述子特征
    frame.curr_kps, frame.curr_des = extract_points(frame)
    # 将角点位置和描述子通过类的属性传递给下一帧作为上一帧的角点信息
    Frame.last_kps, Frame.last_des = frame.curr_kps, frame.curr_des

    if frame.idx == 1:
        # 设置第一帧为初始帧，并以相机坐标系为世界坐标系
        frame.curr_pose = np.eye(4)
        points4d = [[0,0,0,1]]      # 原点为 [0, 0, 0] , 1 表示颜色
    else:
        # 角点配准, 此时会用 RANSAC 过滤掉一些噪声
        match_kps = match_points(frame)
        # 使用八点法拟合出本质矩阵
        essential_matrix = fit_essential_matrix(match_kps)
        print("---------------- Essential Matrix ----------------")
        print(essential_matrix)
        # 利用本质矩阵分解出相机的位姿 Rt
        Rt = extract_Rt(essential_matrix)
        # 计算出当前帧相对于初始帧的相机位姿
        frame.curr_pose = np.dot(Rt, frame.last_pose)
        # 三角测量获得角点的深度信息
        points4d = triangulate(frame.last_kps, frame.curr_kps, frame.last_pose, frame.curr_pose)
		# 判断3D点是否在两个摄像头前方
        good_pt4d = check_points(points4d)
        points4d = points4d[good_pt4d]

        draw_points(frame)
    mapp.add_observation(frame.curr_pose, points4d)     # 将当前的 pose 和点云放入地图中
    # 将当前帧的 pose 信息存储为下一帧的 last_pose 信息
    Frame.last_pose = frame.curr_pose
    return frame