仿射变换（Affine Transformation）是图像处理中很常见的操作，它在数学上可以表述为乘以一个矩阵 (线性变换) 接着再加上一个向量 (平移)。

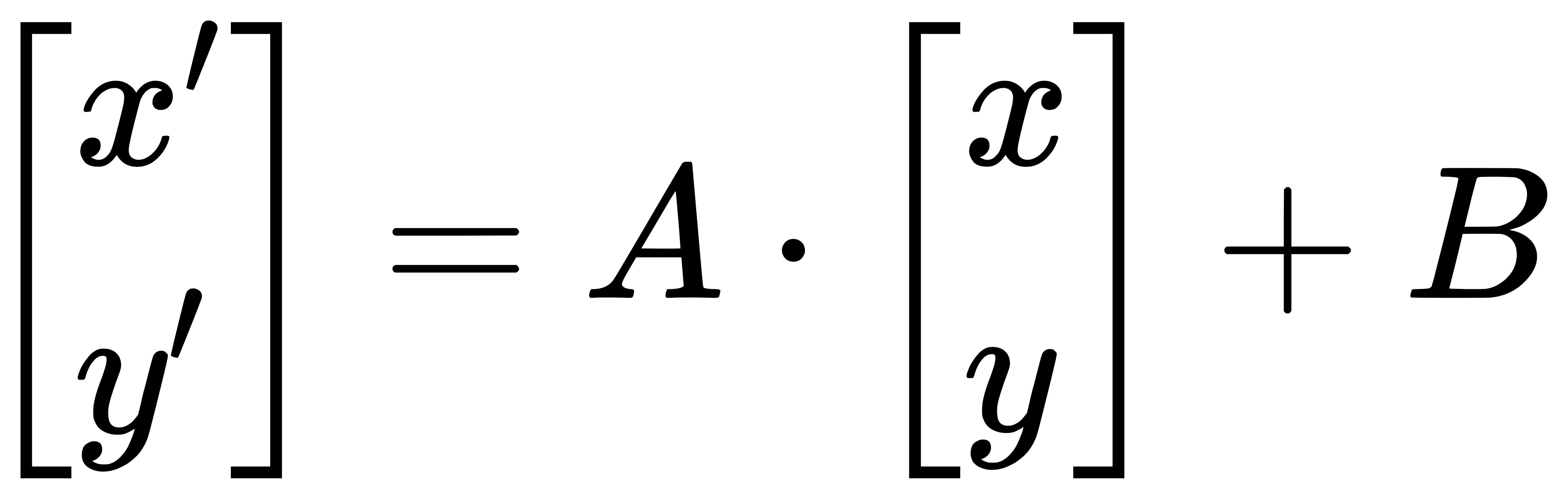
其中：

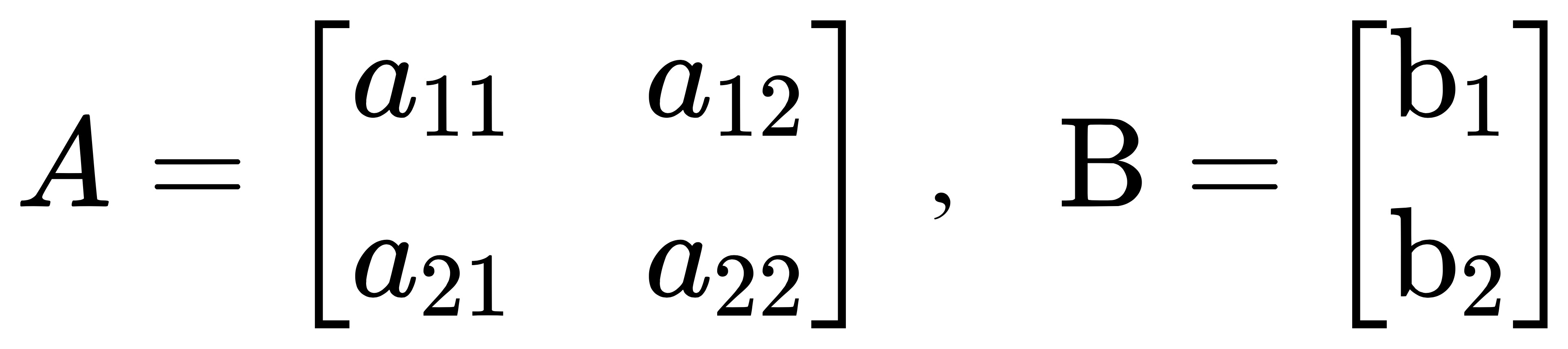
1. 更紧凑的表示

在学术上，更习惯用一个 2x3 的 M 矩阵来表示这层关系，因此得到:

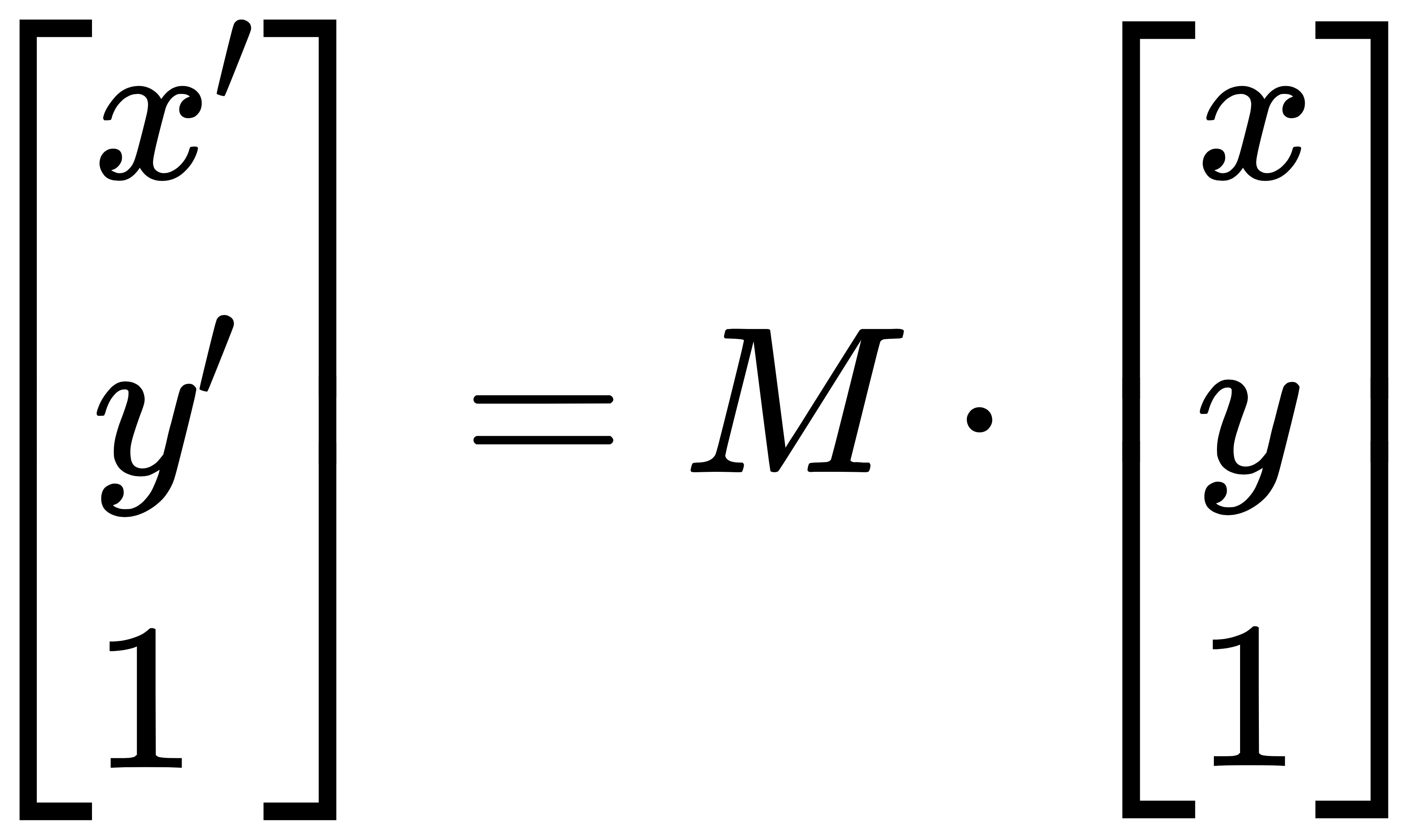
其中：

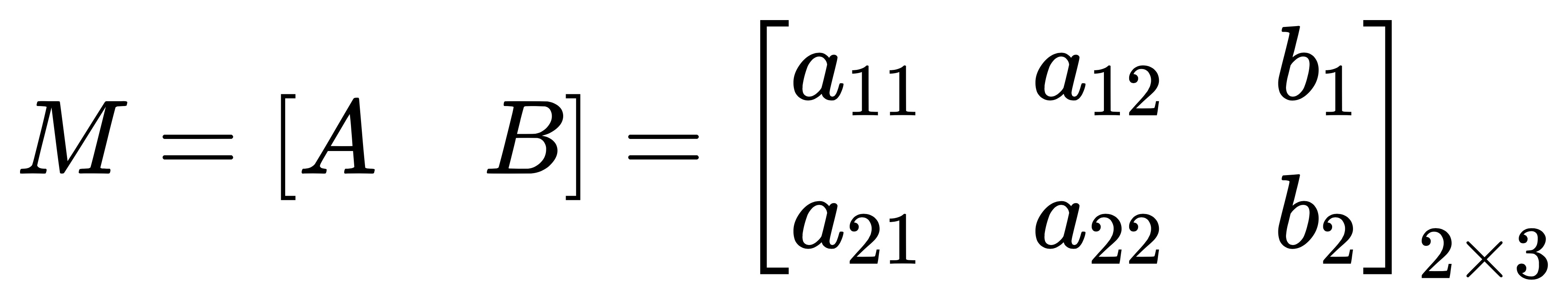
2. 如何求 M ？

如果用线性方程表示它们之间的转换关系，便得到：

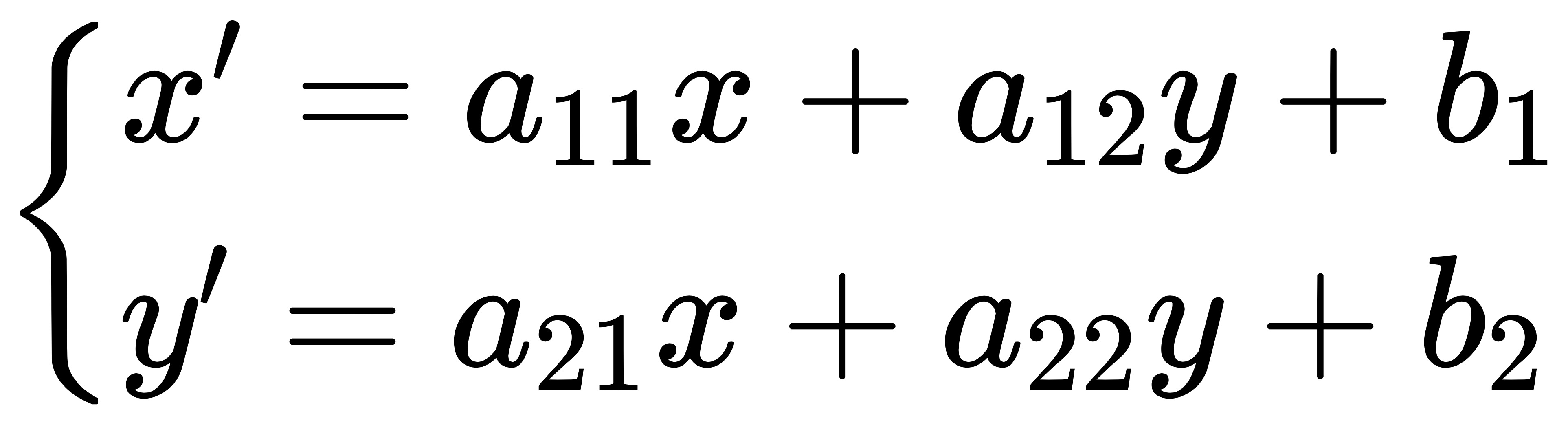
方程中有 6 个未知的参数，如果我们需要求解它们，则至少需要 6 个方程。由于每个像素点都包含了 2 个方程，因此只需要 3 个像素点。好在 OpenCV 提供了函数 cv2.getAffineTransform来根据变换前后 3 个点的对应关系来自动求解 M，例如对于图片

import cv2
import numpy as np

image = cv2.imread("./dog.jpg")
h, w = image.shape[:2]

我们选取图片的三个顶点进行仿射变换，它们分别是左上角：[0, 0]，左下角：[0, h-1]，右上角：[w-1, 0]。

src_points = np.float32([[0, 0], [0, h-1], [w-1, 0]]) 
dst_points = np.float32([[50, 50], [200, h-100], [w-100, 200]]) 
matAffine = cv2.getAffineTransform(src_points, dst_points)

变量matAffine就是仿射变换矩阵 M，如果将它打印出来：

array([[9.38086304e-01, 4.14937759e-02, 5.00000000e+01],
       [3.12695435e-02, 9.17842324e-01, 5.00000000e+01]])

3. 仿射变换

现在可以将刚才求出的仿射变换应用至源图像，使用的是 cv2.warpAffine 函数

affine_result = cv2.warpAffine(image, matAffine, (w,h)) 
cv2.imwrite("affine_result.jpg", affine_result)