手写双目立体匹配 SGM 算法(上)
SGM(Semi-Global Matching)是一个基于双目视觉的半全局立体匹配算法,专门用于计算图像的视差。在 SGM 算法中,匹配代价计算是双目立体匹配的第一步,本文将使用 Census Transform 方法对此进行介绍。
1. 读取图片
首先使用 OpenCV 将左图和右图读取进来,并需要将它们转成单通道的灰度图输出。
import cv2 |

left.png 和 right.png 可以从这里进行下载。
2. 高斯平滑
为了减小双目图片的噪声和细节的层次感,有必要使用高斯平滑算法对它们进行预处理。
left_image = cv2.GaussianBlur(left_image, (3,3), 0, 0) |
3. Census 变换
最早的匹配测度算法使用的是互信息法:对于两幅配准好的影像来说,它们的联合熵是很小的,因为其中一张影像可以通过另外一张影像预测,这表示两者之间的相关性最大,从而互信息也最大。但是它的数学原理非常复杂,且计算需要迭代,计算效率不高。在实际应用中,有一种更简单高效的方法叫 Census 变换更容易收到青睐(OpenCV 里用的就是这种方法)。
Census 变换的基本原理:在图像区域定义一个矩形窗口,用这个矩形窗口遍历整幅图像。选取中心像素作为参考像素,将矩形窗口中每个像素的灰度值与参考像素的灰度值进行比较,灰度值小于参考值的像素标记为 0,大于或等于参考值的像素标记为 1,最后再将它们按位连接,得到变换后的结果,变换后的结果是由 0 和 1 组成的二进制码流。Census 变换的实质是将邻域像素灰度值相对于中心像素灰度值的差异编码成二进制码流。
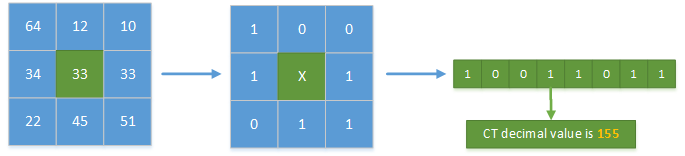
我们不妨首先定义矩形窗口的大小为 7x7,由于不会对图像边界进行填充,因此计算图像的补偿尺寸:
image_h, image_w = left_image.shape[:2] # 获取图片尺寸 |
计算好这些必要的参数后,根据 Census 的变换原理可以获得它们的二进制编码,并将二进制编码存储为十进制数字。整个过程如下所示:
def CensusTransform(image): |
现在利用 CensusTransform 函数对左右图进行变换得到它们的 census 特征
left_census = CensusTransform(left_image) |
我们可以对左图的 Census 特征进行可视化,得到下图所示。
cv2.imwrite("left_census.png", left_census.astype(np.uint8)) |

4. Cost Volume
经过census变换后的图像可以使用汉明距离来计算左右两个匹配点之间相似度,这里并没有使用它们的灰度值,而是它们的 census 序列。这是因为单个像素点的灰度差异进行比较没有多大意义,而用该像素点领域范围内的纹理特征(census 序列)进行比较更具有代表性。
4.1 汉明距离
两个 census 序列之间的相似度比较使用的是 Hamming 距离,它的度量方式为:两个字符串对应位置的不同字符的个数,它本身是一个异或问题,可以使用 numpy.bitwise_xor 进行求解。
| 异或(xor)问题:如果 a、b 两个值不相同,则异或结果为 1。如果 a、b 两个值相同,异或结果为 0。 |
Examples:数字 13 的二进制编码为 00001101, 17 则为 00010001,那么它们之间的 Hamming 距离为:
np.bitwise_xor(13, 17) |
13 和 17 的二进制编码有 3 个字符不同,所以它们的 Hamming 距离为 3。综上来说,Hamming 距离的计算代码如下:
def HanMingDistance(a, b): |
4.2 代价计算
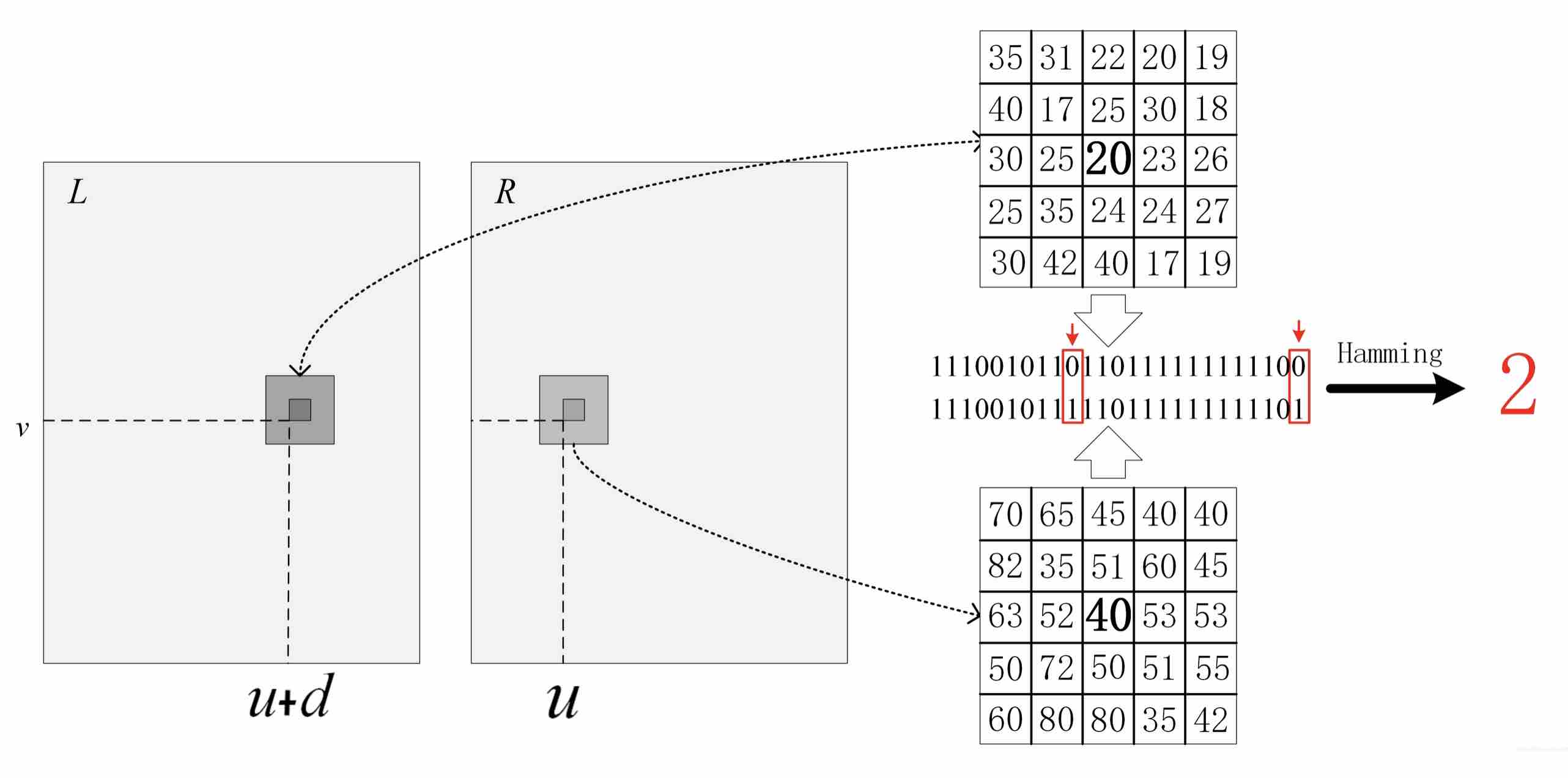
在极线约束下,我们会对右图从左至右进行扫描: 在右图 u 的位置得到该像素的 census 序列,然后与左图 u+d 位置处进行比较。由于我们事先不知道该处的视差到底有多大,因此我们会假设一个最大视差值 max_disparity,并计算 0, 1, 2, ..., max_disparity 处所有的 Hamming 距离。这个过程称为代价计算,如下图所示:
max_disparity = 64 |
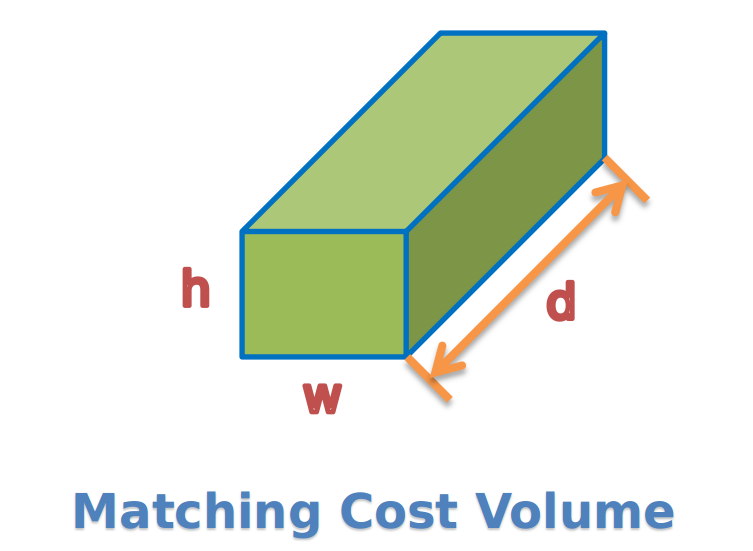
既然现在已经计算出了每个像素在不同视差 d 时的汉明距离,那么其最小值对应的视差理应最接近该像素的真实视差,从而我们可以得到它的视差图并将其进行归一化:
def normalize(disparity_map, max_disparity=64): |

我们可以发现视差图中出现了很多椒盐噪声,因此可以考虑使用中值滤波算法进行去燥,得到下图:

图中的一些连续平面区域依然出现了很多噪声,而且对于视差不连续的区域其效果特别差。因此我们还需要在此基础上加入一些平滑处理,并构造出了一个能量方程。从而使得立体匹配问题可以转换成寻找最优视差图 D,让能量方程 E(D) 取得最小值。
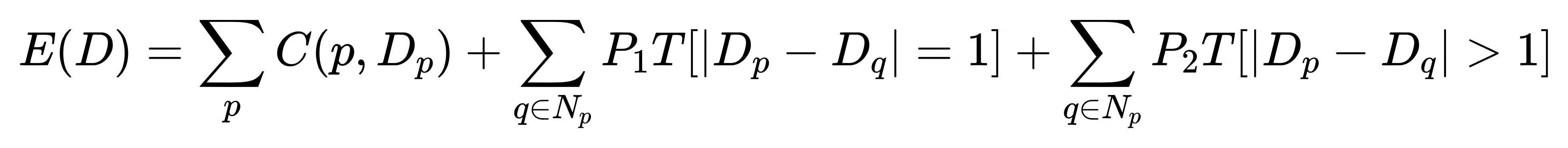
该能量方程由两部分组成:等式右边第一项表示像素点 p 在视差范围内所以匹配代价之和; 第二项和第三项是指当前像素 p 和其邻域内所有像素 q 之间的平滑性约束, 它是 SGM 算法的核心,将在下节对此进行讲述。
参考文献
- [1] Heiko Hirschmuller. stereo Processing by Semi-Global Matching and Mutual Information. CVPR 2005
- [2] LUNOKHOD SGM Blog Post