什么是相机的位姿 ?
在视觉 slam 领域里,相机的位姿是一个特别重要的概念。简单来说,相机的位姿(pose)就是相机的位置和姿态的合称,它描述了世界坐标系与相机坐标系之间的转换关系。
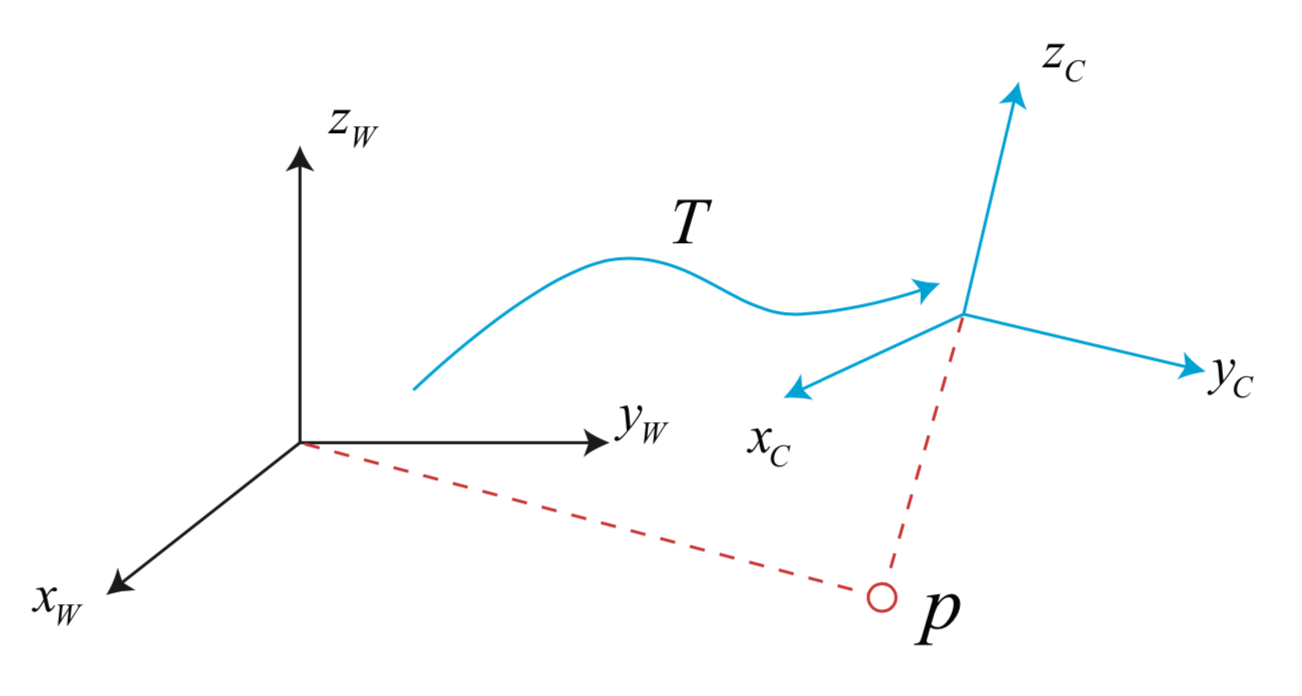
如上图所示:点 P 的世界坐标为 P_{w},可以通过相机的位姿矩阵 T 转换到相机坐标系下为 P_{c} :
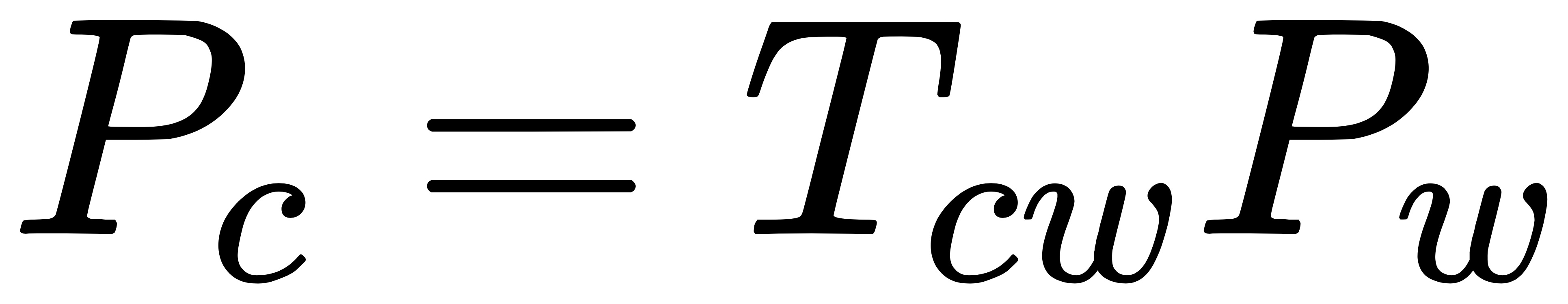
当然你可以将点 P 从相机坐标系转换到世界坐标系中:
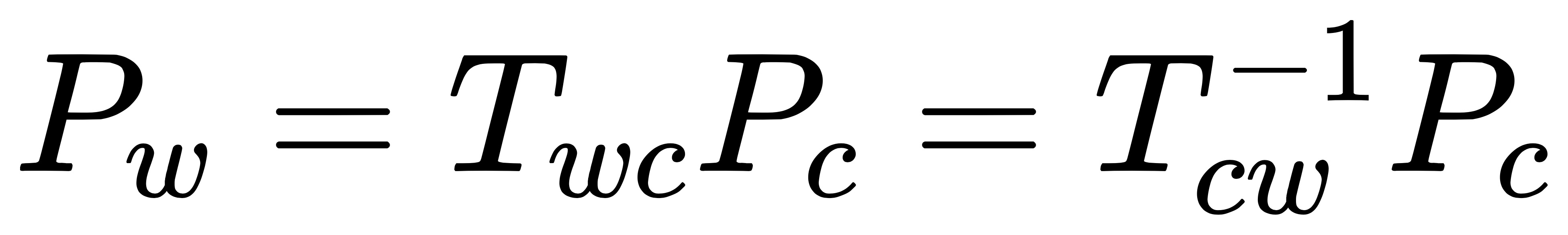
其中 T_{cw} 为该点从世界坐标系变换到相机坐标系的变换矩阵, T_{wc} 为该点从相机坐标系变换到世界坐标系的变换矩阵。它们二者都可以用来表示相机的位姿,前者称为相机的外参。
实践当中使用
T_{cw}来表示相机位姿更加常见。然而在可视化程序中使用T_{wc}来表示相机位姿更为直观,因为此时它的平移向量即为相机原点在世界坐标系中的坐标。视觉 Slam 十四讲中的第五讲的 joinMap 使用的就是T_{wc}来表示相机位姿进行点云拼接。
相机位姿矩阵 T 其实主要由旋转矩阵 R 和平移向量 t 组成:
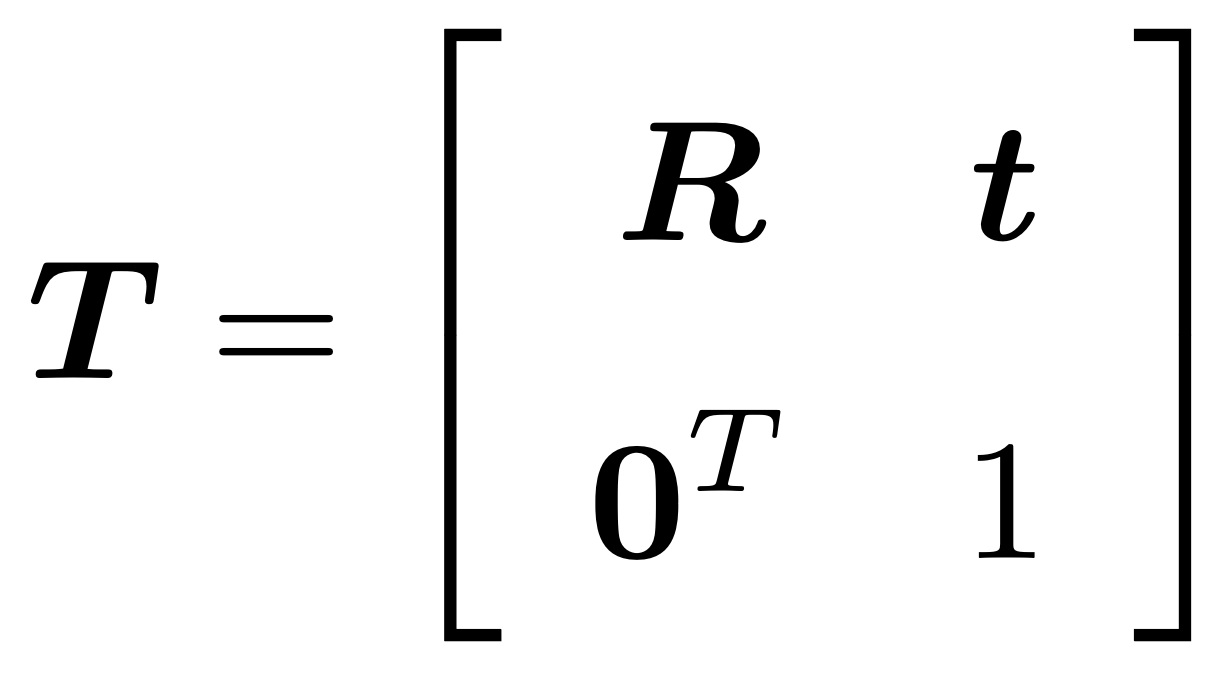
其中旋转矩阵 R 一共有 9 个量,但是一次旋转只有 3 个自由度,因此这种表达方式是冗余的。可以使用欧拉角来描述这种旋转行为,它使用了 3 个分离的转角,把一个旋转分解成了3次绕不同轴的旋转,如下所示:
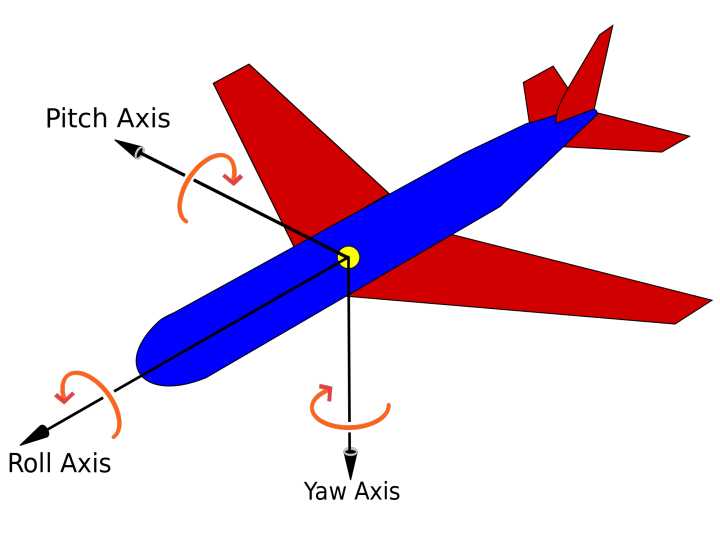
因此旋转矩阵 R 可以由三个转角来表示,它们分别是:
- 偏航角 yaw,绕物体的
Z轴旋转的角度, 用gamma表示; - 俯仰角 pitch,旋转之后绕
Y轴旋转的角度, 用alpha表示; - 滚转角 roll,旋转之后绕
X轴旋转的角度, 用beta表示;
既然欧拉角可以表示物体的旋转状态,那么旋转矩阵 R 应该也能被这个三个角度所表示:首先,旋转矩阵 R 可以被三个矩阵分解得到

其中:
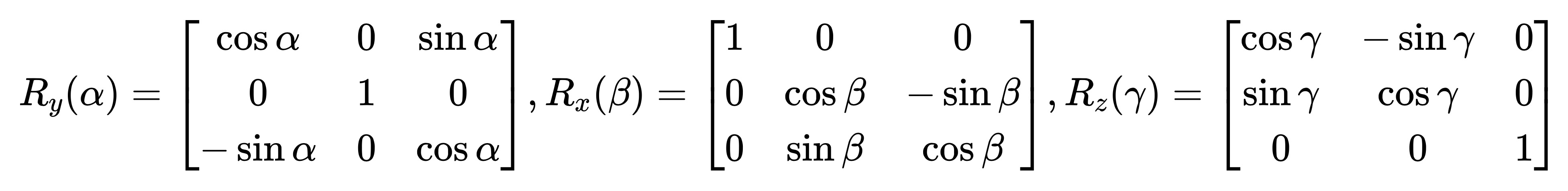
因此它们三者相乘便得到旋转矩阵 R 的表达形式:
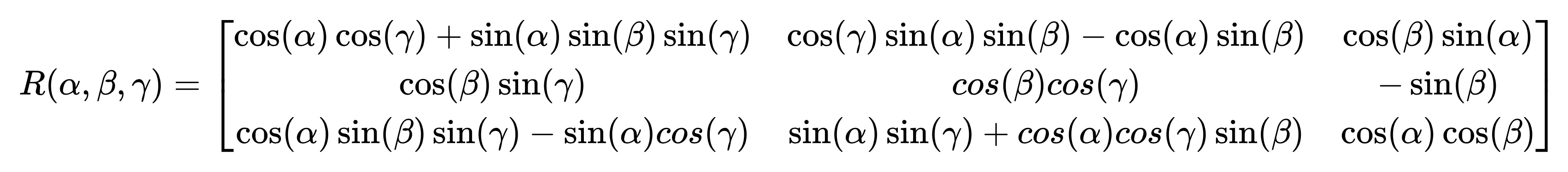
使用这种方法表示的一个重大缺点就是会碰到著名的万向锁问题:在俯仰角为正负 90 度时,第一次旋转与第三次旋转将会使用同一个轴,使得系统失去了一个自由度(由 3 次旋转变成了 2 次旋转)。理论上可以证明,只要想用 3 个实数来表达三维旋转,都不可避免遇到这种问题。
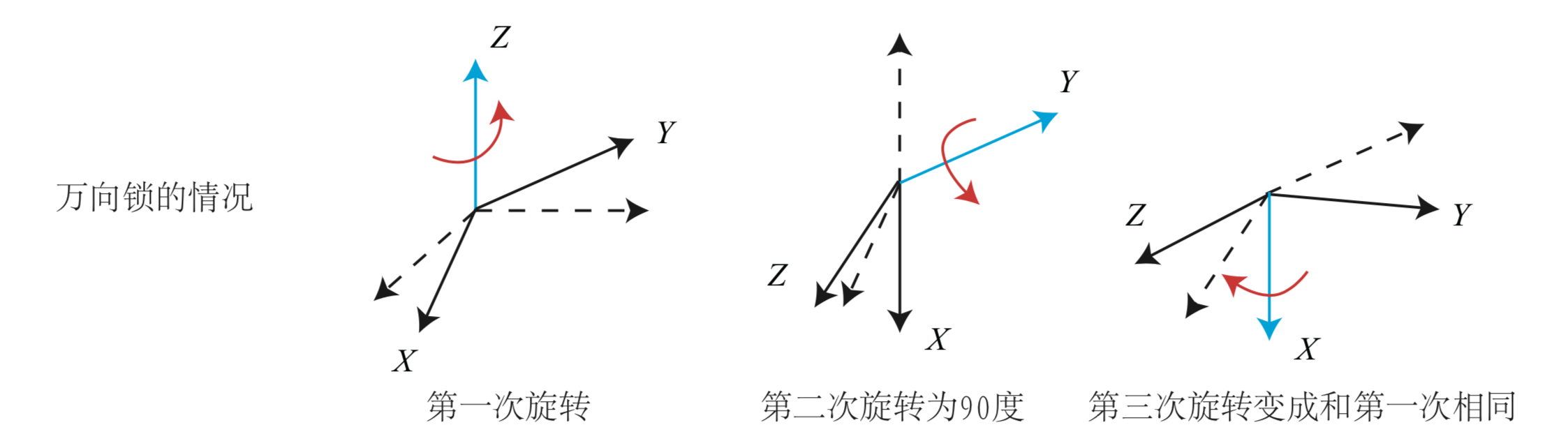
参考文献: