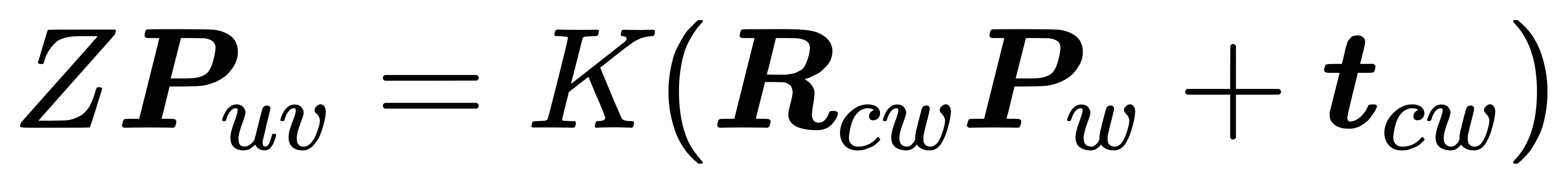相机的内参和外参是立体视觉的基础，今天做个笔记记录下。

1. 相机模型

照片的本质是真实的 3D 场景在相机的成像平面上留下的一个投影，最早的相机是在小孔成像的基础上发展起来的，下面这幅图简单地解释了相机的成像过程。

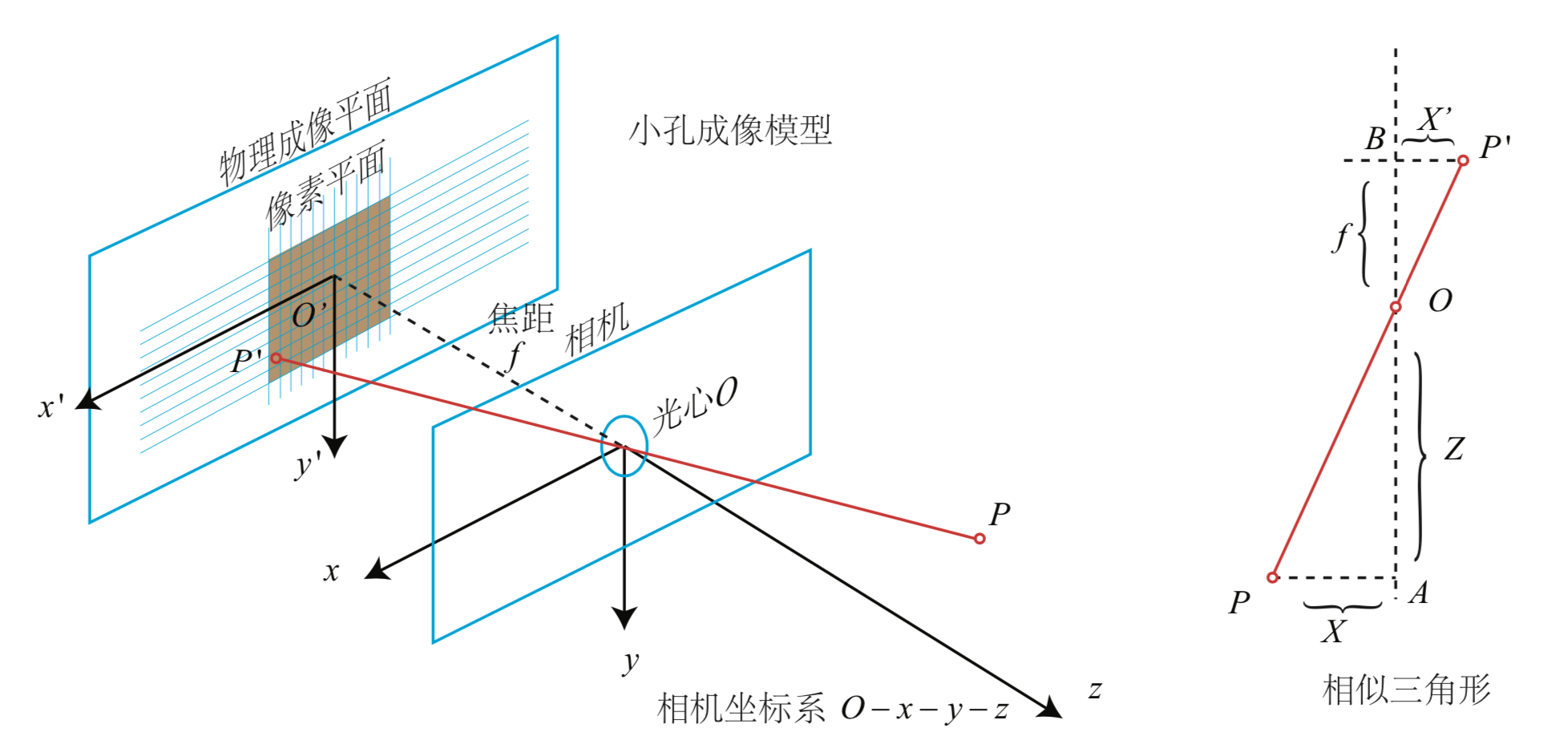
现在来对这个简单的针孔模型进行几何建模。设 O − x − y − z 为相机坐标系，习惯上我们让 z 轴指向相机前方，x 向右，y 向下。O 为摄像机的光心，也是针孔模型中的针孔。现实世界的空间点 P 经过小孔 O 投影之后，落在物理成像平面 O'-x'-y' 上，成像点为 P'。设 P 的坐标为 [X, Y, Z]，P' 为 [x', Y', Z'] 并且设物理成像平面到小孔的距离为 f(焦距)。那么根据三角形相似关系

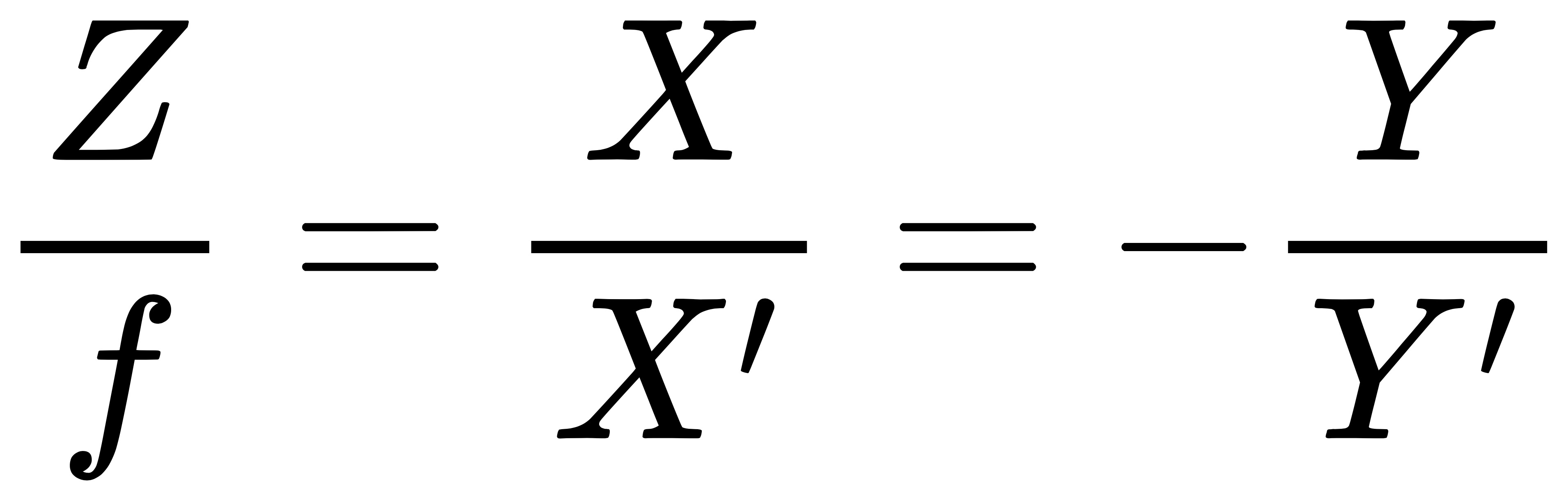
通过整理便得到：

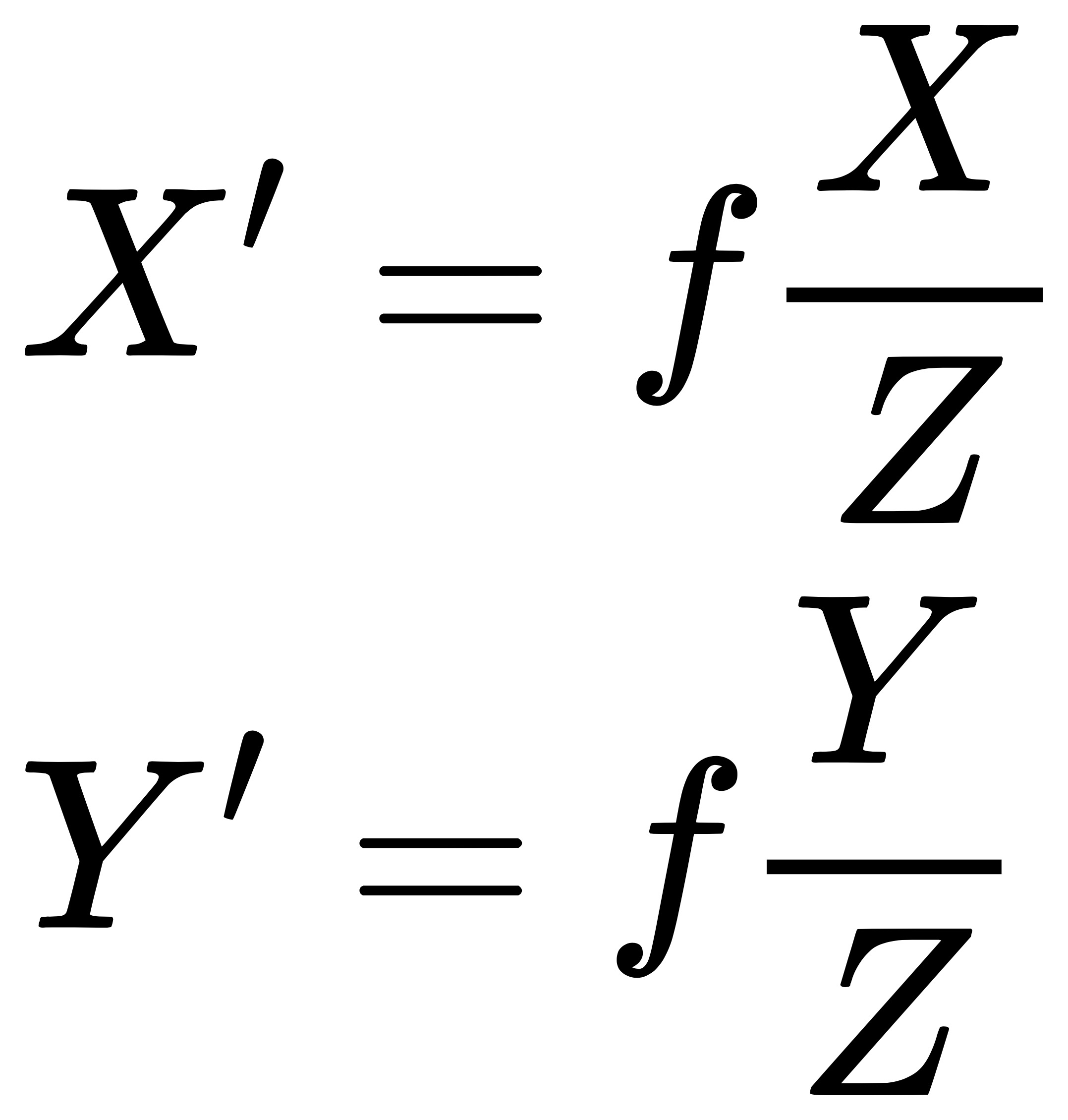
2. 相机内参

上式描述了点 P 和它的像之间的空间关系。不过在相机中，我们最终获得的是 一个个的像素，这需要在成像平面上对像进行采样和量化。

像素坐标系通常的定义方式是：原点 O' 位于图像的左上角，u 轴向右与 x 轴平行，v 轴向下与 y 轴平行。因此，像素坐标系与成像平面之间，相差了一个缩放和一个原点的平移。

我们设像素坐标在 $u$ 轴上缩放了 α 倍，在 v 上缩放了 β 倍。同时，原点平移了 [c_x, c_y]。那么，P' 的坐标与像素坐标 [u, v] 的关系为:

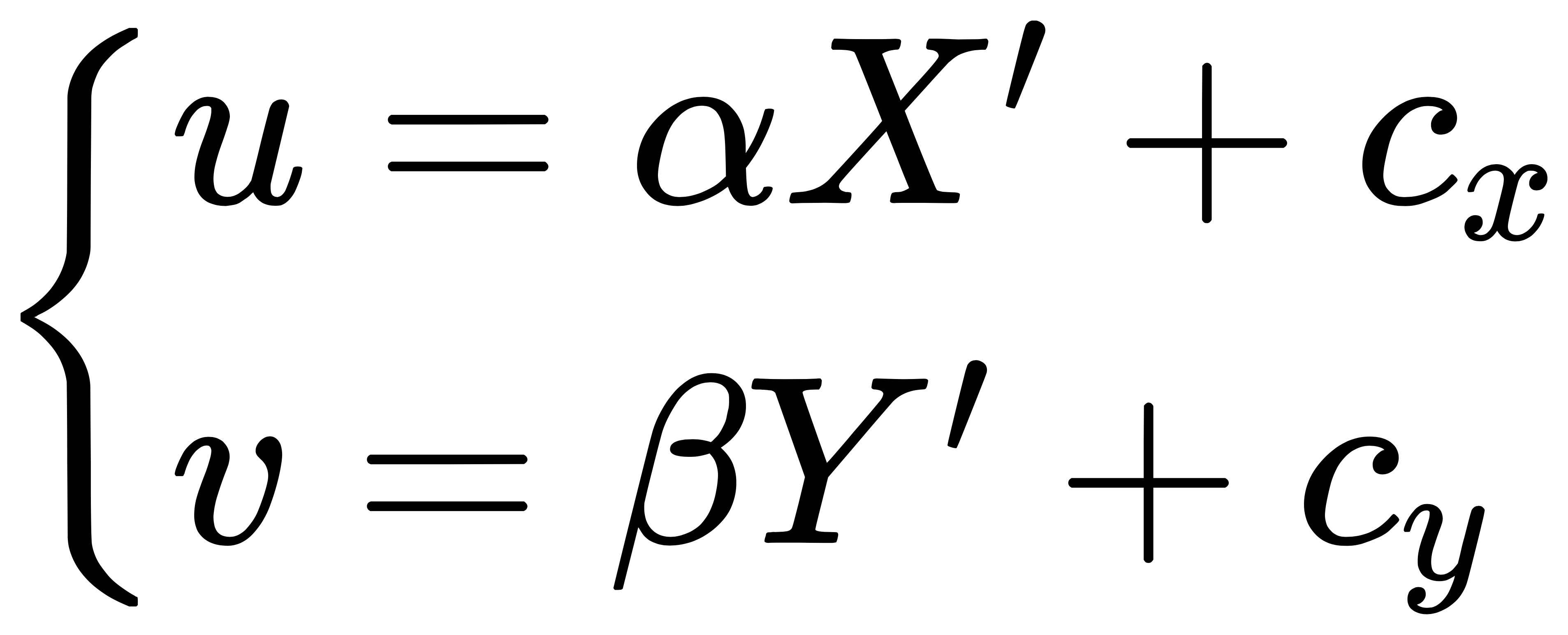
把 αf 合并成 f_{x}，βf 合并成 f_{y}，得:

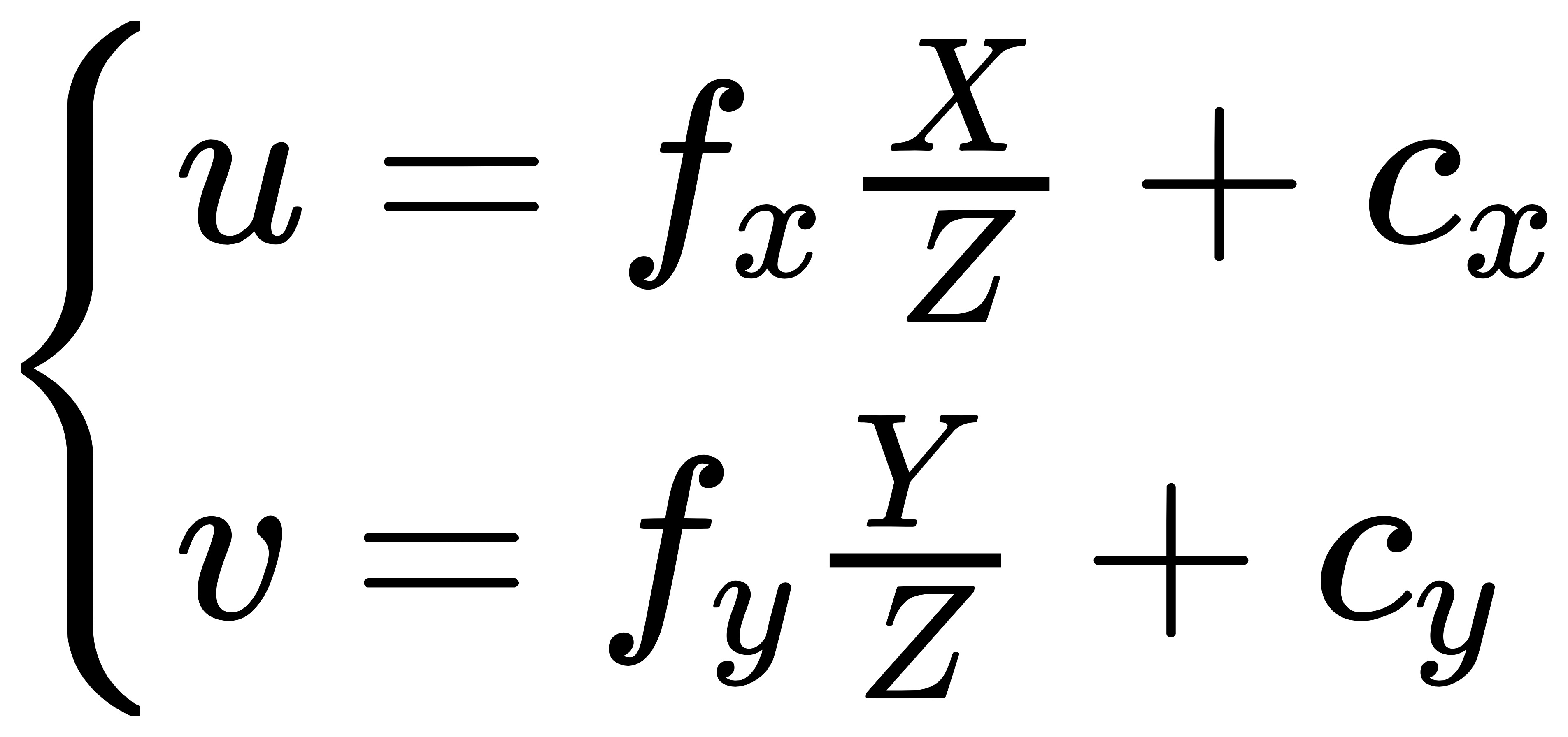
其中，f 的单位为米，α, β 的单位为像素每米，所以 fx , fy 的单位为像素。把该式写成矩阵形式，会更加简洁，不过左侧需要用到齐次坐标:

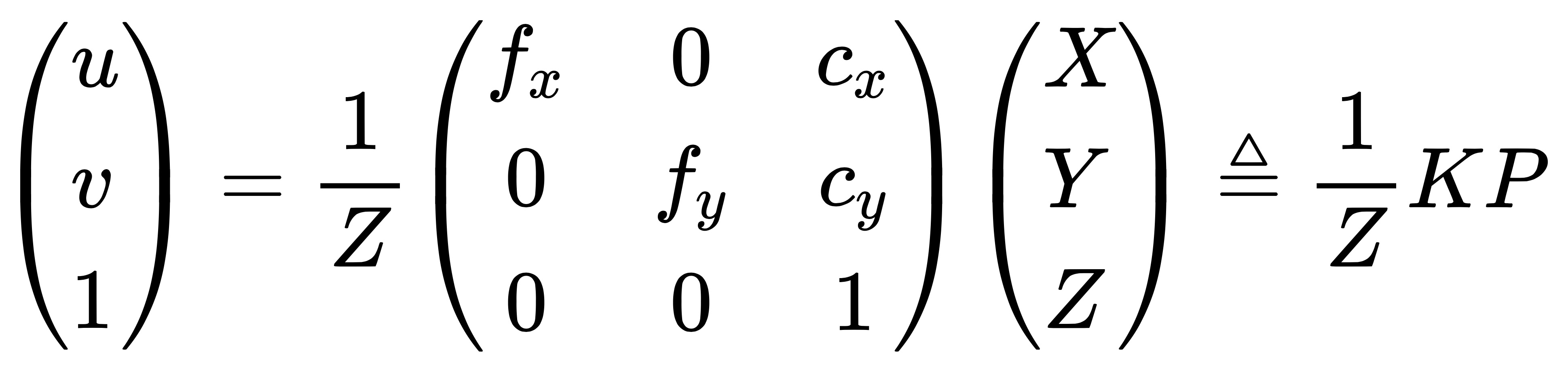
综上，可以整理得到一个非常简洁的公式如下：

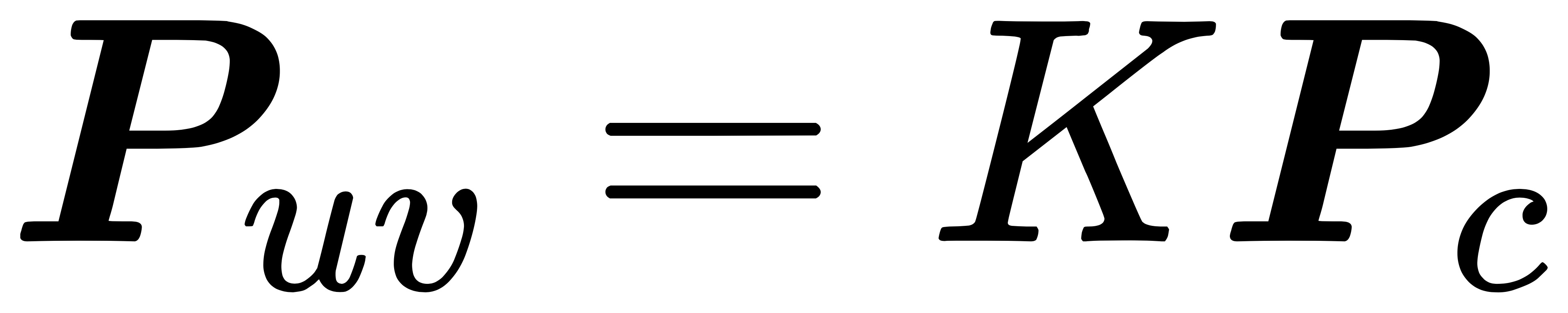
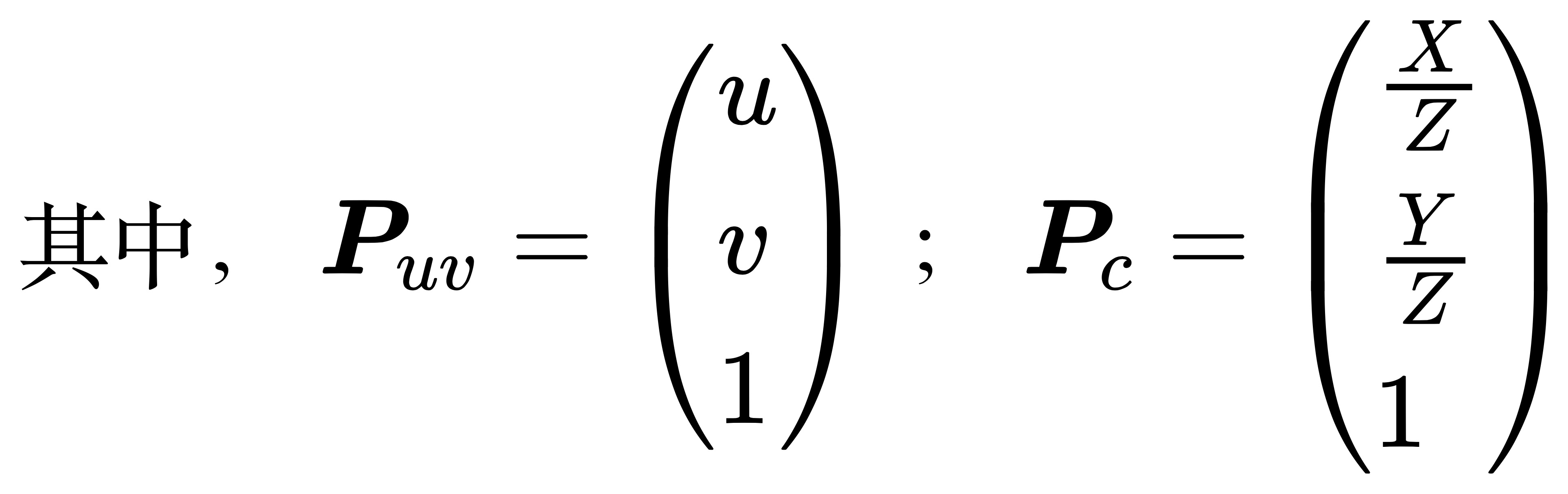
其中，我们把矩阵 K 称为相机的内参(Camera Intrinsics)，它描述了相机坐标系到图像坐标系之间的投影关系。

3. 相机外参

在上面的推导过程中，我们使用的是 P_{c} 在相机坐标系下的坐标。如果我们使用世界坐标系下的 P_{w} 的话，那么就应该使用相机的当前位姿变换到相机坐标系下：

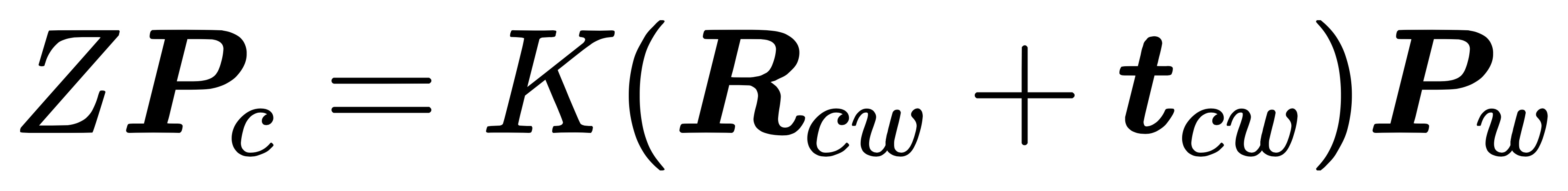
其中，相机的位姿 R, t 又称为相机的外参数 (Camera Extrinsics)，它描述了点 P 的世界坐标到相机坐标的投影关系。因此世界坐标系下点 P 投影到图像坐标系的整个过程为：